A force F = 2 N acts on a particle P in the xz-plane. The force F is parallel to x-axis. The particle P (as shown in the figure) is at a distance 3 m and the line joining P with the origin makes angle $30^{\circ}$ with the x-axis. The magnitude of torque on P with respect to origin O (in N-m) is

A

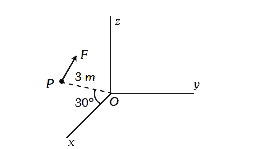
2

B

3

C

4

D

5

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

$F = 2 N, θ = 30^{\circ}, r = 3 m$
$τ = F r sin θ = 2 \times 3 \times {sin 30}^{\circ} \Rightarrow τ = 3$ N-m .

|

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One

A particle mass parallel to x-axis with constant velocity $v$ as shown in the figure. The angular velocity of the particle about the origin O
Aremains constant
Bcontinuously increases
Ccontinuously decreases
Doscillates.
Question 2 - Select One
A particle is moving parallel to x-axis as shown in the figure. The angular velocity of the particle about the origin is
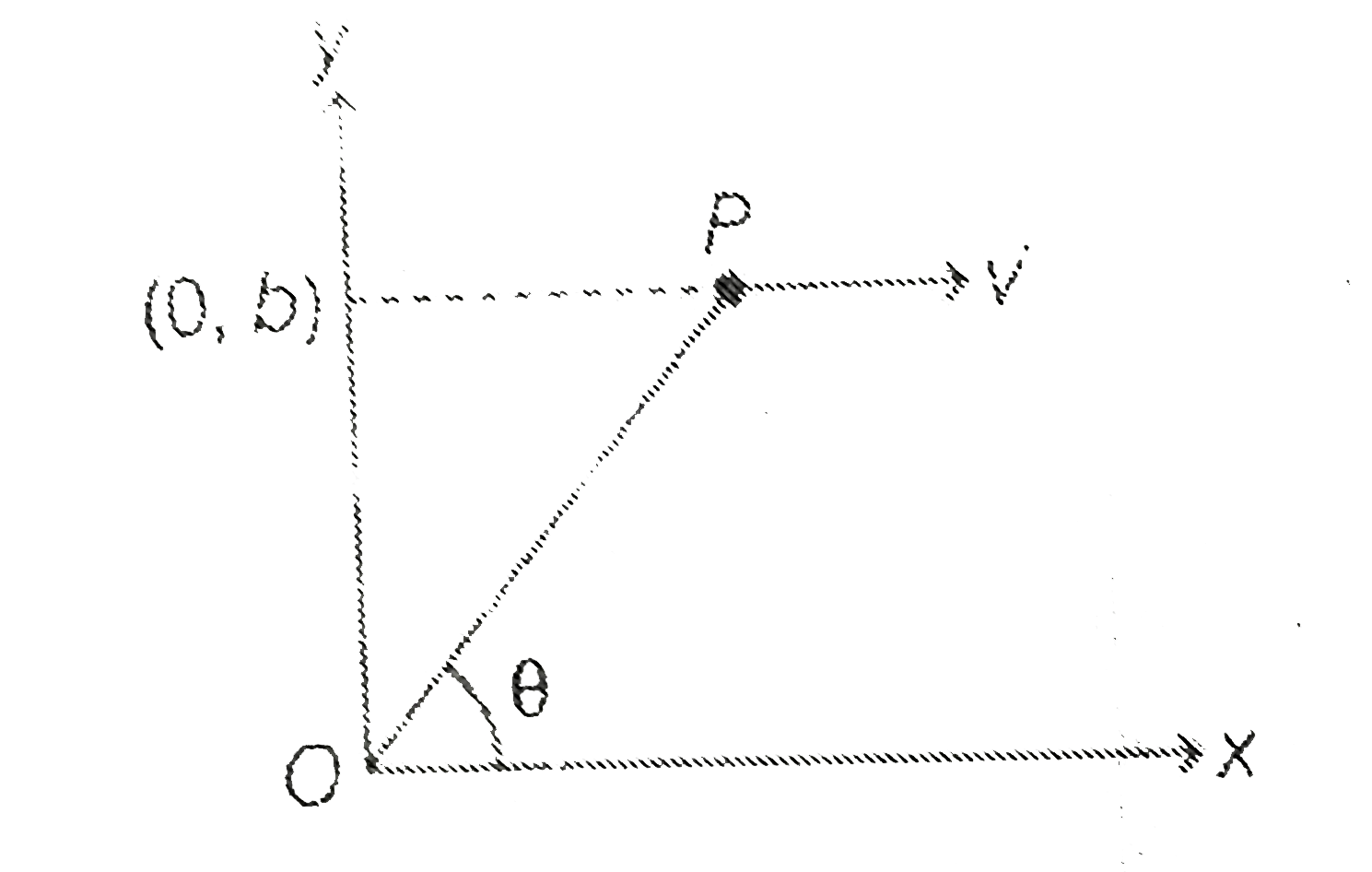A $(v / b) {sin}^{2} θ$
B $(v / b)$
C $(v / b) sin θ$
D $\frac{v}{b sin θ}$
Question 3 - Select One
A particle of mass m is moving with constant velocity v parallel to the x-axis as shown in the figure. Its angular momentum about origin O is

Amvb
Bmva
C $m v \sqrt{a^{2} + b^{2}}$
D $m v (a + b)$

ERRORLESS-ROTATIONAL MOTION-NCERT BASED QUESTIONS (Torque and Couple)

Home
Ask Doubt
Profile