In certain region of space with volume 0.2 m3 the electric potential is found to be 5V throughout. The magnitude of electric field is this region is
Zero
0.5 N / C
1N / C
5 N / C
The correct Answer is:A
Since, electric potential is found throughout constant hence electric field, E=−dVdr=0
Topper's Solved these Questions
- ELECTROSTATICSBOOK - ERRORLESSCHAPTER - ELECTROSTATICSEXERCISE - ASSERTION & REASON
25 Videos
- ELECTROSTATICSBOOK - ERRORLESSCHAPTER - ELECTROSTATICSEXERCISE - NCERT BASED QUESTIONS (Grouping of Capacitors)
58 Videos
- ELECTRONICSBOOK - ERRORLESSCHAPTER - ELECTRONICSEXERCISE - Assertion & Reason
26 Videos
- MAGNETIC EFFECTS OF CURRENT BOOK - ERRORLESSCHAPTER - MAGNETIC EFFECTS OF CURRENT EXERCISE - ASSERTION & REASON
18 Videos
Similar Questions
Knowledge Check
In certain region of space with volume 0.2 m3 the electric potential is found to be 5V throughout. The magnitude of electric field is this region is
A0.5N/CB1N/CC5N/CDzeroIn a certain 0.1m3 of space, electric potential is found to be 5 V throughout. What is the electric field in this region ?
A50V/mBzeroC0.5V/mDNone of theseIn a certain region of space the electric potential V is known to be constant. Is the electric field in this region (a) positive (b) zero ,or (c ) negative ?
AAlso constantBPositiveCNegativeDZero
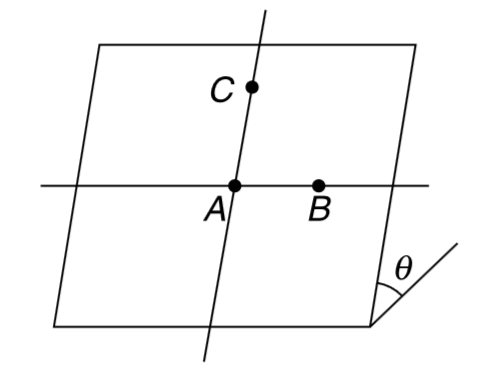
It is known that there exists a uniform electric field in a certain region. Imagine an incline plane (figure) in the region which is inclined at θ=37∘ to the horizontal when one moves horizontally along the incline from A to B (AB=1cm), the electric potential decreases by 10V. Similarly, potential at C(AC=1cm) is less than potential at A by 10 V where line AC lies on the incline and is perpendicualr to AB. When one moves vertically up from point A to a point D(AD=1cm), the potential drop by 10 V again. Find the magnitude of the electric field in the region and the angle that it makes with vertical [given sin37∘=35]
View SolutionIn a certain region of space, the potential field depends on x and y-coordinates as V=(−x2+y2). The corresponding electric field lines in xy-plane are correctly represented by
View SolutionElectric potential at any point is V=−5x+3y+√15z, then the magnitude of the electric field is
View SolutionElectric potential at any point is V=−5x+3y+√15z, then the magnitude of the electric field is
View SolutionIn a certain region of space, the electric field is zero. From this, we can conclude that the electric potential in this region is:
View Solution
