In Figure 2, AB and AC are tangents to the circle with centre O such that angle BAC = 40°. Then angle BOC is equal to
To solve the problem, we need to find the angle BOC given that AB and AC are tangents to the circle with center O, and angle BAC = 40°.
1. Identify the Tangents and Angles:
- We have two tangents, AB and AC, drawn from point A to the circle.
- The angle between these tangents is given as angle BAC = 40°.
2. Understand the Properties of Tangents:
- The radius of the circle at the point of tangency is perpendicular to the tangent line.
- Therefore, OB (radius) is perpendicular to AB, and OC (radius) is perpendicular to AC.
- This means angle OBA = 90° and angle OCA = 90°.
3. Set Up the Equation for the Angles:
- The angles around point O in quadrilateral ABOC can be expressed as:
Angle OBA+Angle BAC+Angle ACO+Angle BOC=360°
- Substituting the known angles:
90°+40°+90°+Angle BOC=360°
4. Combine the Known Angles:
- Adding the known angles together:
90°+40°+90°=220°
- Thus, we can rewrite the equation as:
220°+Angle BOC=360°
5. Solve for Angle BOC:
- Rearranging the equation to isolate angle BOC:
Angle BOC=360°−220°=140°
6. Conclusion:
- Therefore, the angle BOC is equal to 140°.
Final Answer:
Angle BOC = 140°
- We have two tangents, AB and AC, drawn from point A to the circle.
- The angle between these tangents is given as angle BAC = 40°.
- The radius of the circle at the point of tangency is perpendicular to the tangent line.
- Therefore, OB (radius) is perpendicular to AB, and OC (radius) is perpendicular to AC.
- This means angle OBA = 90° and angle OCA = 90°.
- The angles around point O in quadrilateral ABOC can be expressed as:
Angle OBA+Angle BAC+Angle ACO+Angle BOC=360°
- Substituting the known angles:
90°+40°+90°+Angle BOC=360°
- Adding the known angles together:
90°+40°+90°=220°
- Thus, we can rewrite the equation as:
220°+Angle BOC=360°
- Rearranging the equation to isolate angle BOC:
Angle BOC=360°−220°=140°
- Therefore, the angle BOC is equal to 140°.
Angle BOC = 140°
Topper's Solved these Questions
Similar Questions
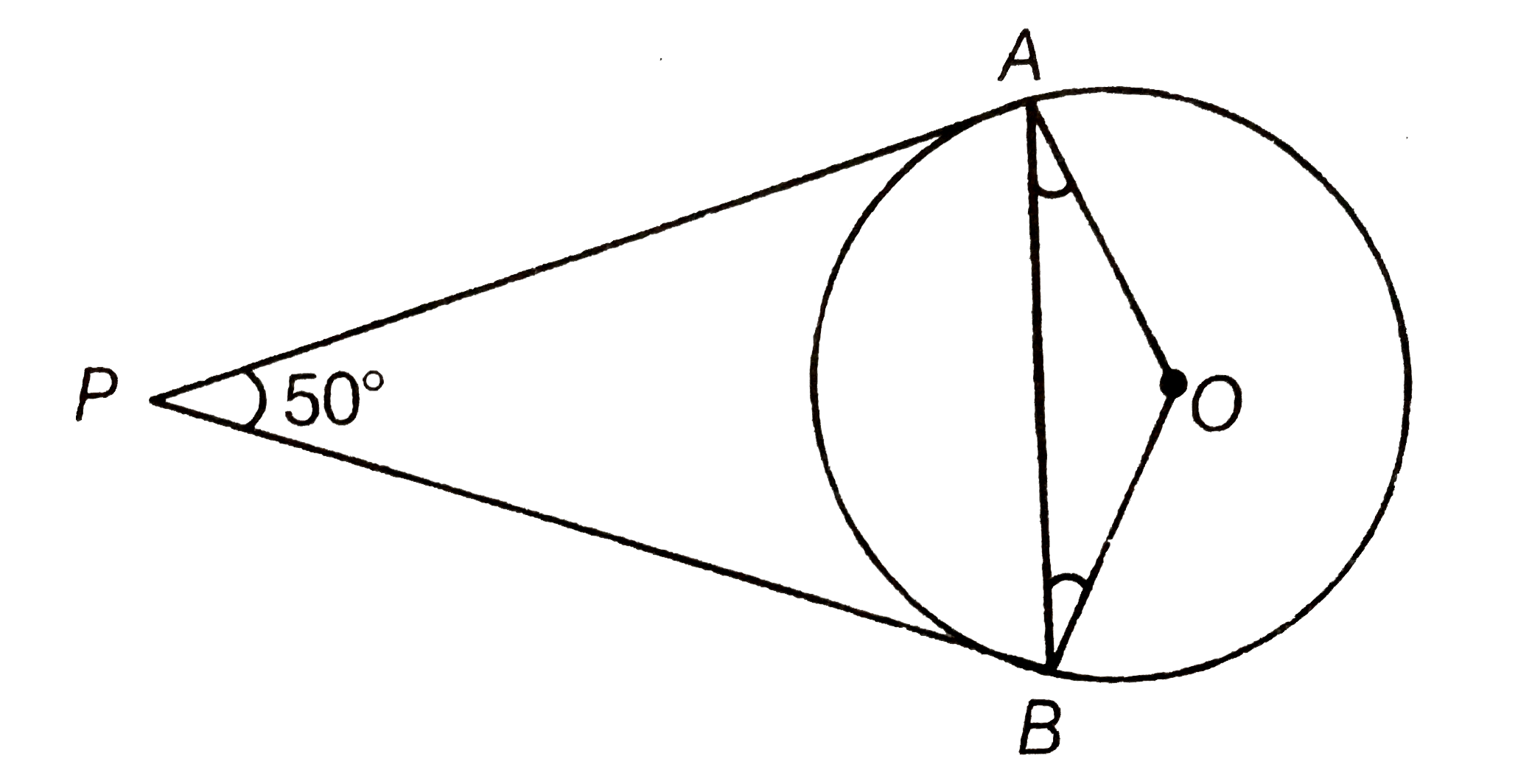
In figure, if PA and PB are tangents to the circle with centre O such that ∠APB=50∘, then ∠OAB is equal to
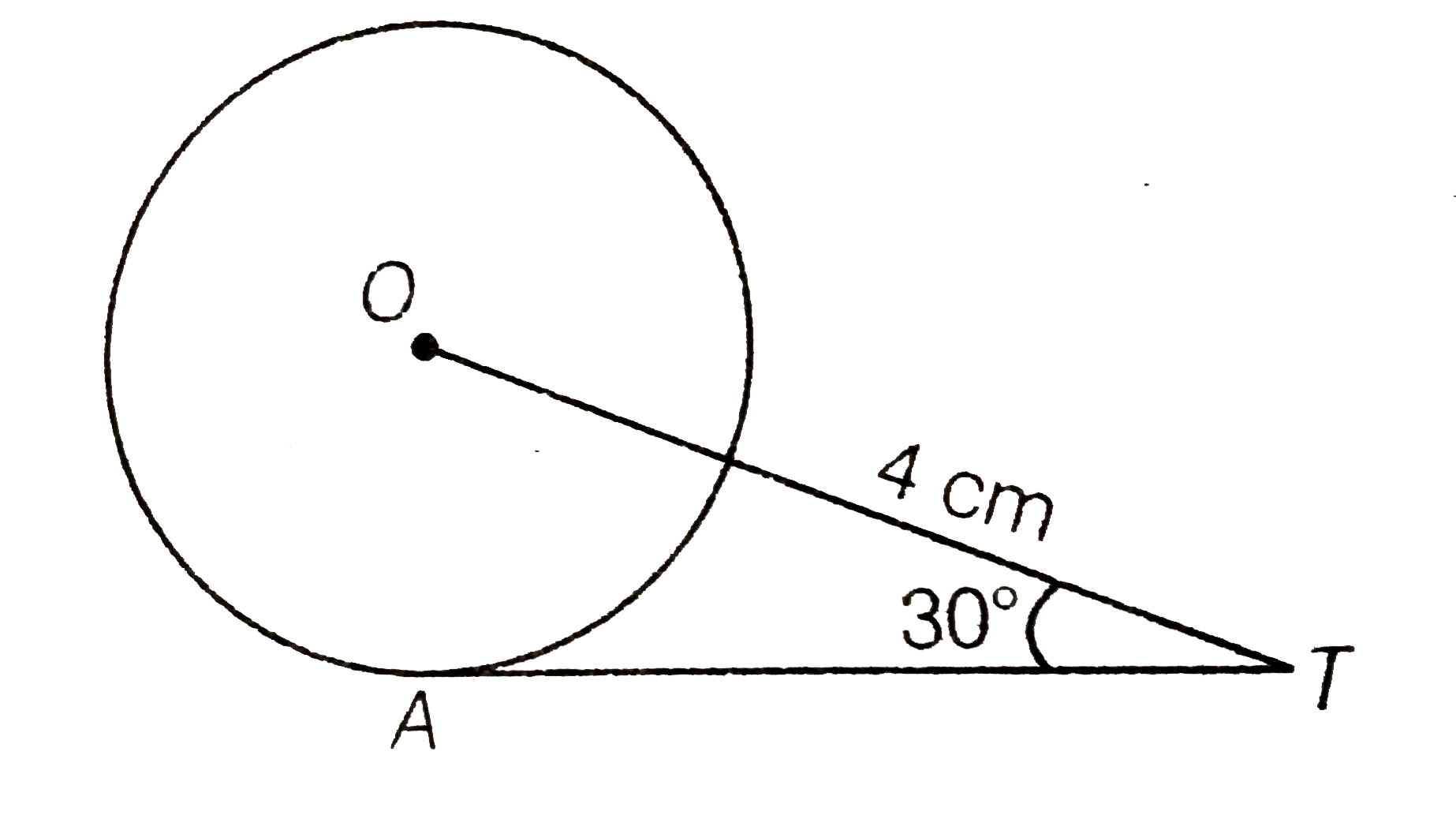
View SolutionIn figure, AT is a tangent to the circle with centre O such that OT = 4 cm and ∠OTA=30∘. Then, AT is equal to
View SolutionIn the given figure, if TP and TQ are tangents to a circle with centre O, so that ∠POQ=110∘, then ∠PTQ is
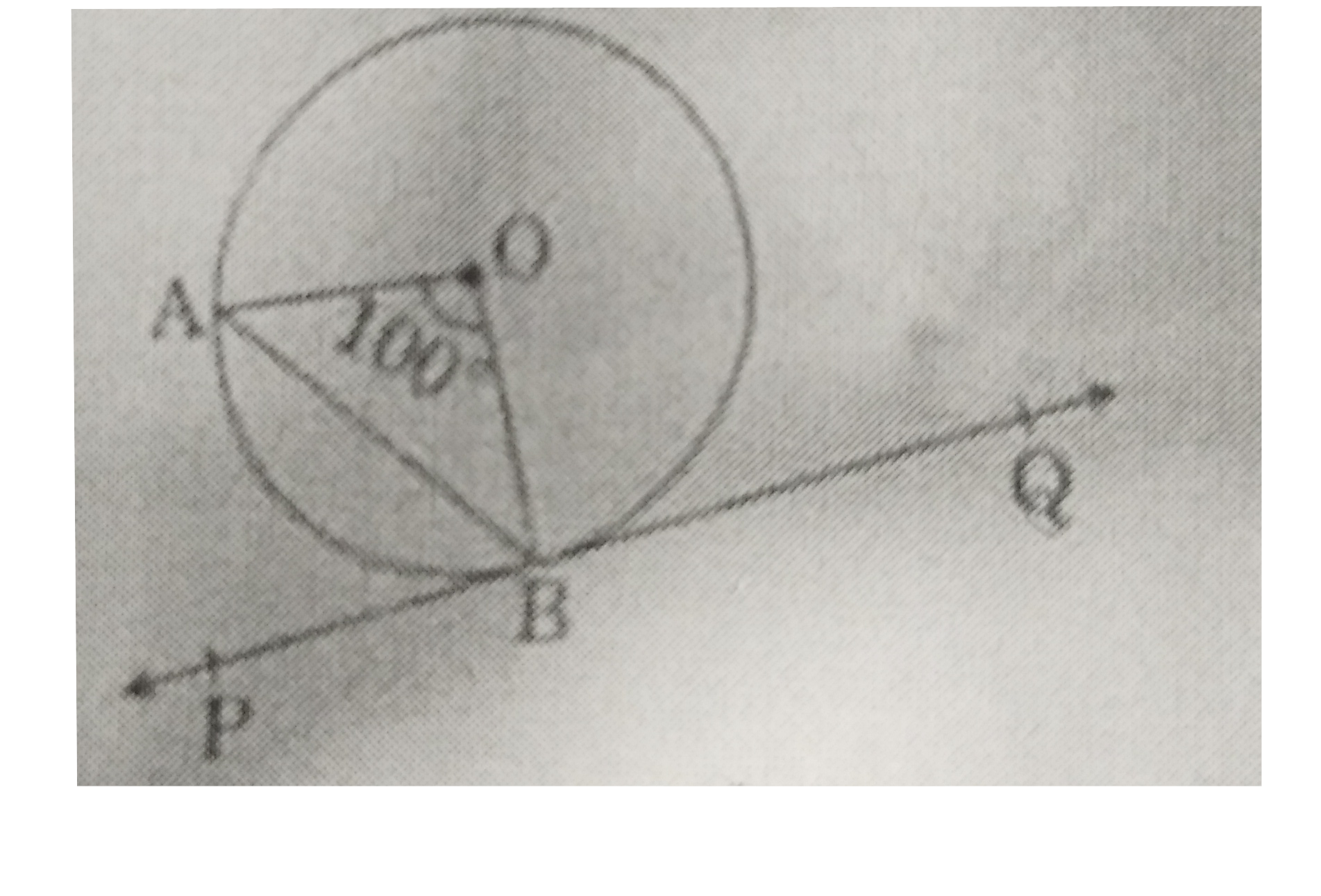
View SolutionIn figure PQ is tangent to the circle with centre at O at the point B , if ∠AOB=100∘, then ∠ABP is equal to

View SolutionIn Figure-2 PQ is tangent to the circle with centre at O , at the point B. If ∠AOB = 100∘ , then ∠ABP is equal to
(A) 50∘
(B) 40∘
(C) 60∘
(D) 80∘
View SolutionIn figure-3, PQ is tangent to the circle with centre at O, at the point B. if ∠AOB=100∘, then ∠ABP is equal to
View SolutionAB is the diameter and AC is a chord of a circle with centre O such that angle BAC=30∘. The tangent to the circle at C intersects AB produced in D. Show that BC=BD.
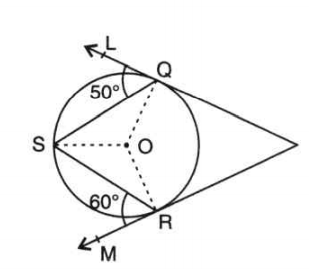
View SolutionIn the given figure, PQL and PRM are two tangents to the circle with centre O at the point Q and R respectively. If S is a point on the circle such that angle SQL = 50° and sk... o angle SRM = 60°. Find the reflex angle QOR.
View SolutionIn the given figure AC is a tangent to the circle with centre O.
If ∠ADB=55∘, find x and y. Give reason for your answer.
View SolutionIf tangents PA and PB from a point P to a circle with centre O are inclined to each other at angle of 80∘, then ∠POA is equal to
View Solution
