A body starting from rest, accelerates at a constant rate a m/s2 for some time after which it decelerates at a constant rate b m/s2 to come to rest finally. If the total time elapsed is t sec, the maximum velocity attained by the body is given by
aba+btm/s
aba−btm/s
2aba+btm/s
2aba−btm/s
The correct Answer is:A
To solve the problem of finding the maximum velocity attained by a body that starts from rest, accelerates at a constant rate am/s2 for some time, and then decelerates at a constant rate bm/s2 to come to rest, we can break down the solution into several steps.
1. Define Variables:
- Let T1 be the time during which the body accelerates.
- Let T2 be the time during which the body decelerates.
- The total time T is given by:
T=T1+T2
2. Use the First Equation of Motion for Acceleration:
- Since the body starts from rest, the initial velocity u=0.
- The final velocity after accelerating for time T1 is given by:
Vmax=u+aT1=0+aT1=aT1
- This is our Equation 1.
3. Use the First Equation of Motion for Deceleration:
- The body comes to rest after decelerating, so the final velocity v=0.
- The initial velocity for this phase is Vmax.
- The equation for deceleration gives:
0=Vmax−bT2⟹Vmax=bT2
- This is our Equation 2.
4. Relate T1 and T2:
- From Equation 1 and Equation 2, we can equate Vmax:
aT1=bT2
- Rearranging gives:
T1=bT2a
5. Substitute T1 in Total Time Equation:
- Substitute T1 into the total time equation:
T=T1+T2=bT2a+T2
- Factoring out T2:
T=T2(ba+1)=T2(b+aa)
- Solving for T2:
T2=Taa+b
6. Substitute T2 back to find Vmax:
- Substitute T2 into Equation 2:
Vmax=bT2=b(Taa+b)=abTa+b
Final Result:
The maximum velocity attained by the body is given by:
Vmax=abTa+b
- Let T1 be the time during which the body accelerates.
- Let T2 be the time during which the body decelerates.
- The total time T is given by:
T=T1+T2
- Since the body starts from rest, the initial velocity u=0.
- The final velocity after accelerating for time T1 is given by:
Vmax=u+aT1=0+aT1=aT1
- This is our Equation 1.
- The body comes to rest after decelerating, so the final velocity v=0.
- The initial velocity for this phase is Vmax.
- The equation for deceleration gives:
0=Vmax−bT2⟹Vmax=bT2
- This is our Equation 2.
- From Equation 1 and Equation 2, we can equate Vmax:
aT1=bT2
- Rearranging gives:
T1=bT2a
- Substitute T1 into the total time equation:
T=T1+T2=bT2a+T2
- Factoring out T2:
T=T2(ba+1)=T2(b+aa)
- Solving for T2:
T2=Taa+b
- Substitute T2 into Equation 2:
Vmax=bT2=b(Taa+b)=abTa+b
The maximum velocity attained by the body is given by:
Vmax=abTa+b
Topper's Solved these Questions
- MOTION IN ONE DIMENSIONBOOK - ERRORLESSCHAPTER - MOTION IN ONE DIMENSIONEXERCISE - NCERT BASED QUESTIONS (RELATIVE MOTION )
18 Videos
- MOTION IN ONE DIMENSIONBOOK - ERRORLESSCHAPTER - MOTION IN ONE DIMENSIONEXERCISE - NCERT BASED QUESTIONS (MOTION UNDER GRAVITY )
56 Videos
- MOTION IN ONE DIMENSIONBOOK - ERRORLESSCHAPTER - MOTION IN ONE DIMENSIONEXERCISE - NCERT BASED QUESTIONS (UNIFORM MOTION )
24 Videos
- KINETIC THEORY OF GASES BOOK - ERRORLESSCHAPTER - KINETIC THEORY OF GASES EXERCISE - ASSERTION AND REASON
16 Videos
- MOTION IN TWO DIMENSIONBOOK - ERRORLESSCHAPTER - MOTION IN TWO DIMENSIONEXERCISE - ASSERTION & REASON
19 Videos
Similar Questions
A car acceleration form rest at a constant rate α for some time, after which it decelerates at a constant rate β, to come to rest. If the total time elapsed is t evaluate (a) the maximum velocity attained and (b) the total distance travelled.
View SolutionA car accelerates from rest at a constant rate α for some time, after which it decelerates at a constant rate β, to come to rest. If the total time elapsed is t seconds. Then evalute (a) the maximum velocity reached and (b) the total distance travelled.
View Solution
Knowledge Check
A car accelerates from rest at a constant rate for some time after which it decelerates at a constant rate β to come to rest. If the total time elapsed is t, the maximum velocity acquired by the car is given by :
Aαβα+βtBα+βαβtCα2+β2βαDα+β2βαA car accelerates from rest at a constant rate α for sometime , after which it decelerates at a constant rate β and comes to rest. If T is the total time elapsed, the maximum velocity acquired by the car is
A(αβα+β)TB((α+βαβ)TC(α2+β2αβ)TD12αTβA car accelerates from rest at a constant rate for some time after which it decelerates at a constant rate β to come to rest. If the total time elapsed is t, the maximum velocity acquired by the car is given by :
Aab(a+b)tBab(a−b)tCat2(a+b)Dtb2(a+b)
A car accelerates from rest at a constant rate α for some time, after which it decelerates at a constant rate β and ultimately comes to rest.If the total time-lapse is t, what is the total distance described and maximum velocity reached ?
View Solution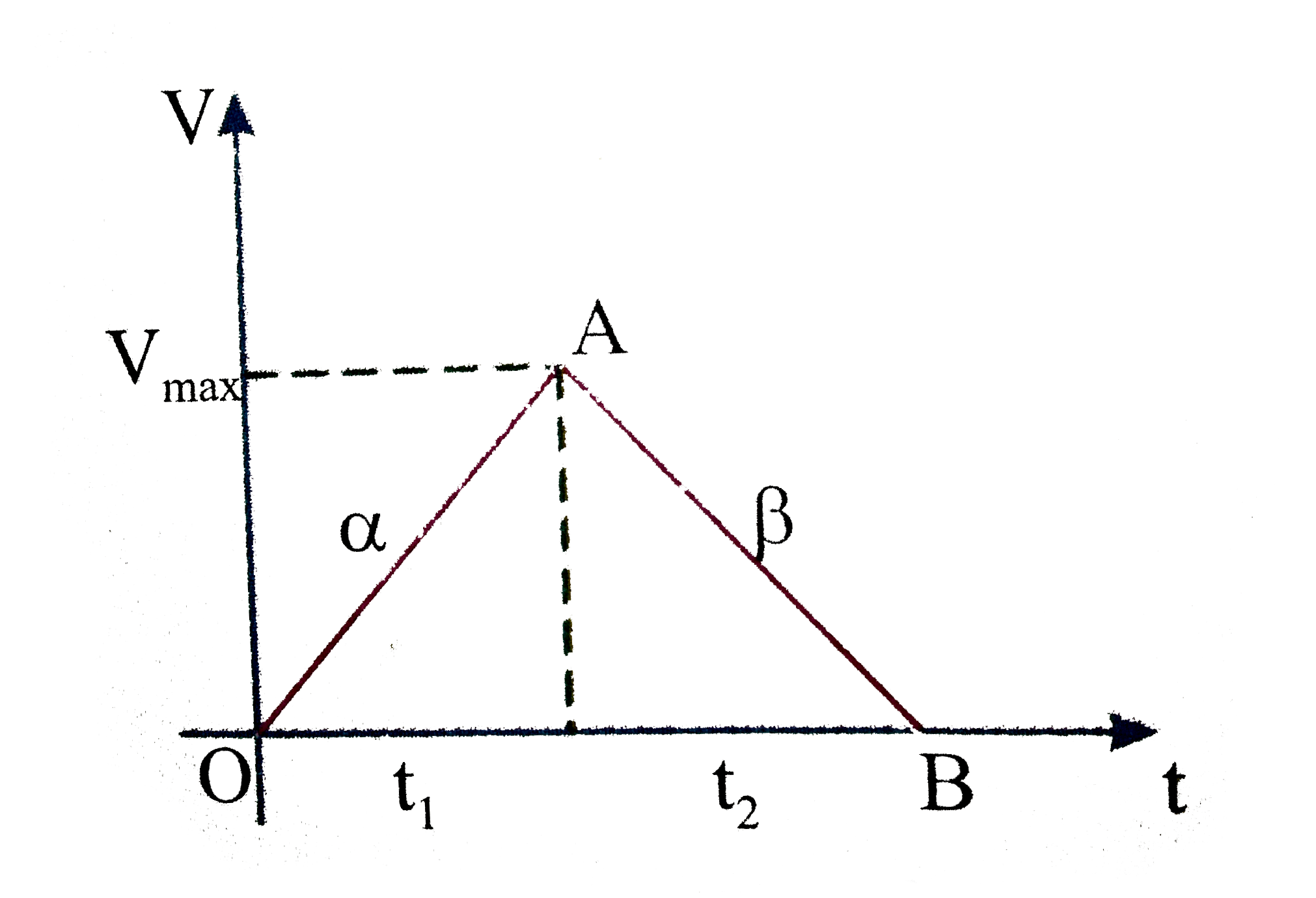
A bus accelerated from rest at a constant rate α for some time, after which it decelerates at a constant rate β to come to rest. If the total time elapsed is t seconds. Then evaluate following parameters from the given graph
(a) the maximum velocity achieved.
(b) the total distance travelled graphically and
(c) Average velocity.
View SolutionA car accelerates from rest at acionstant rate 36kmh∘ to comet to rest. If the total time elapsed id 1 hour, calculate (i) the maximum velocity attained by the car and (ii) the total distance travelled by car.
View SolutionA car acceleration from rest at a constant rate 2m/s2 for some time. Then, it retards at a constant rate of 4m/s2 and comes to rest. If it remains motion for 3 second, then the maximum speed attained by the car is:-
View SolutionA car accelerates from rest at a constant rate of 2ms−2 for some time. The it retatds at a constant rate of 4ms−2 and comes to rest. It remains in motion for 6s.
View Solution
