A rope of mass 0.1 kg is connected at the same height of two opposite walls. It is allowed to hang under its own weight. At the contact point between the rope and the wall, the rope makes an angle θ=10∘ with respect to horizontal. The tension in the rope at its midpoint between the wall is
2.78 N
2.56 N
2.82 N
2 .71 N
The correct Answer is:C
To solve the problem of finding the tension in the rope at its midpoint, we will follow these steps:
Step 1: Understand the Setup
We have a rope of mass m=0.1kg hanging between two walls, making an angle θ=10∘ with the horizontal. The rope is in static equilibrium under the influence of its weight.
Step 2: Identify Forces Acting on the Rope
The weight of the rope acts downwards at its midpoint. The weight W of the rope can be calculated using the formula:
W=mg
where g is the acceleration due to gravity, approximately 9.8m/s2.
Step 3: Calculate the Weight of the Rope
Substituting the values:
W=0.1kg×9.8m/s2=0.98N
Step 4: Analyze the Tension Components
At the midpoint of the rope, the tension T has two components:
- A vertical component Tsinθ
- A horizontal component Tcosθ
Since the rope is in equilibrium, the vertical components of the tension must balance the weight of the rope:
2Tsinθ=W
Here, 2Tsinθ accounts for the contributions from both sides of the rope.
Step 5: Substitute the Weight into the Equation
Now, substituting W:
2Tsinθ=0.98N
Step 6: Solve for Tension T
Rearranging the equation gives:
T=0.982sinθ
Step 7: Calculate sinθ
For θ=10∘, we can use a calculator or trigonometric tables to find:
sin10∘≈0.1736
Step 8: Substitute sinθ into the Tension Equation
Now, substituting sin10∘:
T=0.982×0.1736≈0.980.3472≈2.83N
Step 9: Conclusion
Thus, the tension in the rope at its midpoint is approximately:
T≈2.83N
We have a rope of mass m=0.1kg hanging between two walls, making an angle θ=10∘ with the horizontal. The rope is in static equilibrium under the influence of its weight.
The weight of the rope acts downwards at its midpoint. The weight W of the rope can be calculated using the formula:
W=mg
where g is the acceleration due to gravity, approximately 9.8m/s2.
Substituting the values:
W=0.1kg×9.8m/s2=0.98N
At the midpoint of the rope, the tension T has two components:
- A vertical component Tsinθ
- A horizontal component Tcosθ
2Tsinθ=W
Here, 2Tsinθ accounts for the contributions from both sides of the rope.
Now, substituting W:
2Tsinθ=0.98N
Rearranging the equation gives:
T=0.982sinθ
For θ=10∘, we can use a calculator or trigonometric tables to find:
sin10∘≈0.1736
Now, substituting sin10∘:
T=0.982×0.1736≈0.980.3472≈2.83N
Thus, the tension in the rope at its midpoint is approximately:
T≈2.83N
Topper's Solved these Questions
- BOOK - ERRORLESSCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - NCERT BASED QUESTION (THIRD LAW OF MOTION)11videos
NEWTON'S LAWS OF MOTION
- BOOK - ERRORLESSCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - NCERT BASED QUESTION (CONSERVATION OF LINEAR MOMENTUM AND IMPULSE)29videos
NEWTON'S LAWS OF MOTION
- BOOK - ERRORLESSCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - ASSERTION & REASON18videos
NEWTON'S LAWS OF MOTION
- BOOK - ERRORLESSCHAPTER - MOTION IN TWO DIMENSIONEXERCISE - ASSERTION & REASON19videos
MOTION IN TWO DIMENSION
- BOOK - ERRORLESSCHAPTER - ROTATIONAL MOTIONEXERCISE - Assertion & Reason25videos
ROTATIONAL MOTION
Similar Questions
A wooden block of mass 100 kg rests on a flat wooden floor, the coefficient of friction between the two being 0.4. The block by a rope making an angle of 30∘ with the horizontal. What is the minimum tension along the rope that just makes the rope sliding?
View SolutionA block of mass M is pulled along a horizontal frictionless surface by a rope of mass m as shown in A horizontal force F is applied to one end of the rope. Find
(a) the acceleration of the rope and block
(b) the force that the rope exerts on the block
(c) the tension in the rope at its mid point
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A rope of mass 0.2 kg is connected at the same height of two opposite walls. It is allowed to hang under its own weight. At the contact point between the rope and the wall, the rope makes an angle θ=30%∘ with respect to horizontal. The tension in the rope at its midpoint between the walls is
A1.78 NB1.56 NC1.82 ND1.96 N - Question 2 - Select One
The tops of two poles of height 60 metres and 35 metres are connected by a rope. If the rope makes an angle with the horizontal whose tangent is 5/9 metres, then what is the distance (in metres) between the two poles?
A63B30C25D45 - Question 3 - Select One
A mass M is suspended by a rope from a rigid support at A as shown in figure. Another rupe is tied at the end B, and it is pulled horizontally with a force. If the rope AB makes an angle θ with the vertical in equilibrium then the tension in the string AB is
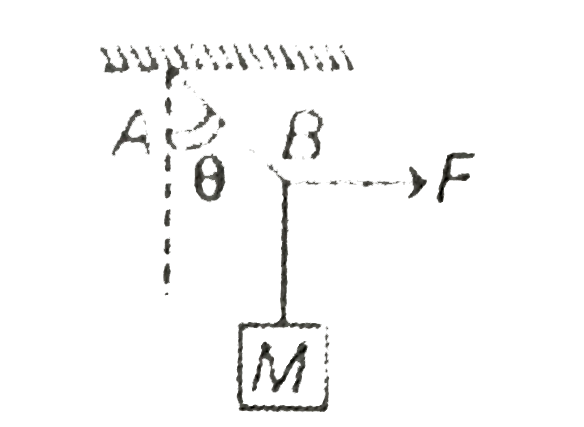 AF sinθBF/sinθCFcosθDF/cosθ
AF sinθBF/sinθCFcosθDF/cosθ
A 40 kg mass, hanging at the end fo a rope of length l, oscillates in a vertical plane with an angular amplitude θ0. What is the tension in the rope when it makes en angle θ with the vertical ? If the breaking strength of the rope is 80kg, what is the maximum amplitude with which the mass can oscillate without the rope breaking?
View SolutionA rope of mass m is hung from a ceiling. The centre point is pulled down with a vertical force F. The tangent to the rope at its ends makes an angle α with horizontal ceiling. The two tangents at the lower point make an angle of θ with each other. Find θ .
 View Solution
View SolutionA ball of mass m is suspended from a rope of length L. It describes a horizontal circle of radius r with speed v. the rope makes an angle θ with vertical given by sinθ=r/2. Determine (a) the tension in the rope and (b) the speed of the ball. (c) time period of ball.
View SolutionA rope of length L has its mass per unit langth λ varies according to the function λ(x)=ex/L. The rope is pulled by a constant force of 1 N on a smooth horizontal surface. The tension in the rope at x=L/2 is :
 View Solution
View SolutionOn a pulley of mass M hangs a rope with two masses m1 and m2(m1>m2) tied at the ends as shown in the figure. The pulley rotates without any friction, whereas the friction between the rope and the pulley is large enough to prevent any slipping. Which of the following plots best represents the difference between the tensions in the rope on the two sides of the pulley as a function of the mass of the pulley ?
 View Solution
View Solution

