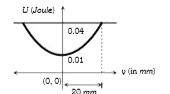
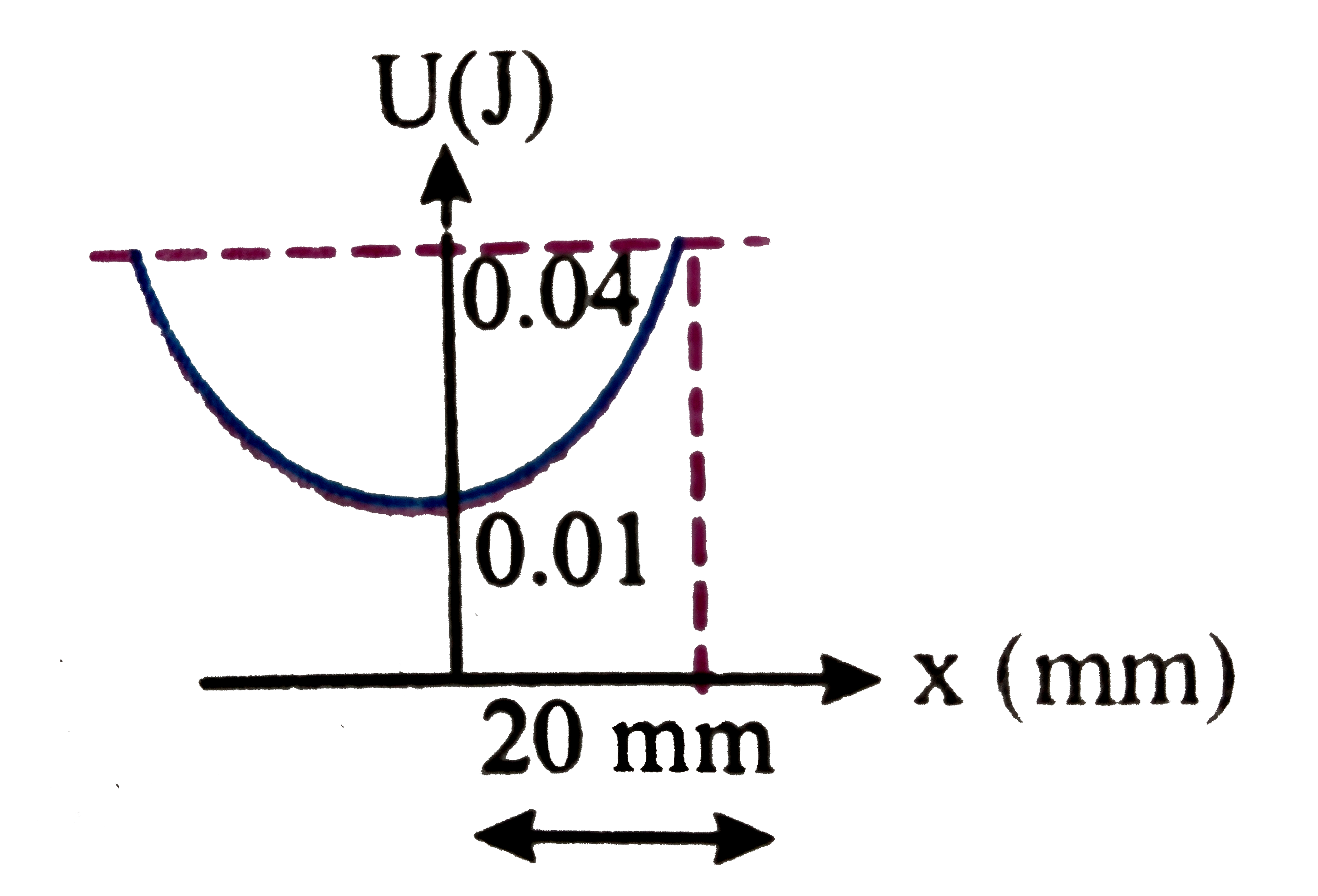
The variation of potential enegy of harmonic oscillator is as shown in figure. The spring constant is
1×102N/m
150N/m
0.667×102N/m
3×102N/m
The correct Answer is:B
(PE)Total=0.04J
Resting PE=0.01 J
Maximum KE=0.04-0.01=0.03 J
⇒0.03=12mω2A2=12kA2
0.03=12×k(201000)2⇒k=150N/m.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - ERRORLESSCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - NCERT BASED QUESTIONS (Time Period and Frequency)
7 Videos
- SIMPLE HARMONIC MOTIONBOOK - ERRORLESSCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - NCERT BASED QUESTIONS (Simple Pendulum)
27 Videos
- SIMPLE HARMONIC MOTIONBOOK - ERRORLESSCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - NCERT BASED QUESTIONS (Acceleration of Simple Harmonic Motion)
11 Videos
- ROTATIONAL MOTIONBOOK - ERRORLESSCHAPTER - ROTATIONAL MOTIONEXERCISE - Assertion & Reason
25 Videos
- SURFACE TENSIONBOOK - ERRORLESSCHAPTER - SURFACE TENSIONEXERCISE - ASSERTION & REASON
11 Videos
Similar Questions
At which position the potential energy of a harmonic oscillator is maximum or minimum ?
View SolutionA body of mass 0.4 kg is held between two massless springs whose ends are fixed to rigid walls as shown in the figure. The spring constants are 8 N/m and 2 N/m. If the body is displaced along the direction of the lengths of the springs and released, the time period (in second) of the oscillations will be (ignore vertical oscillation, if any )

View Solution
Knowledge Check
The veriation of potential energy of harmonic escillator is as shown in figure. The spring constant is
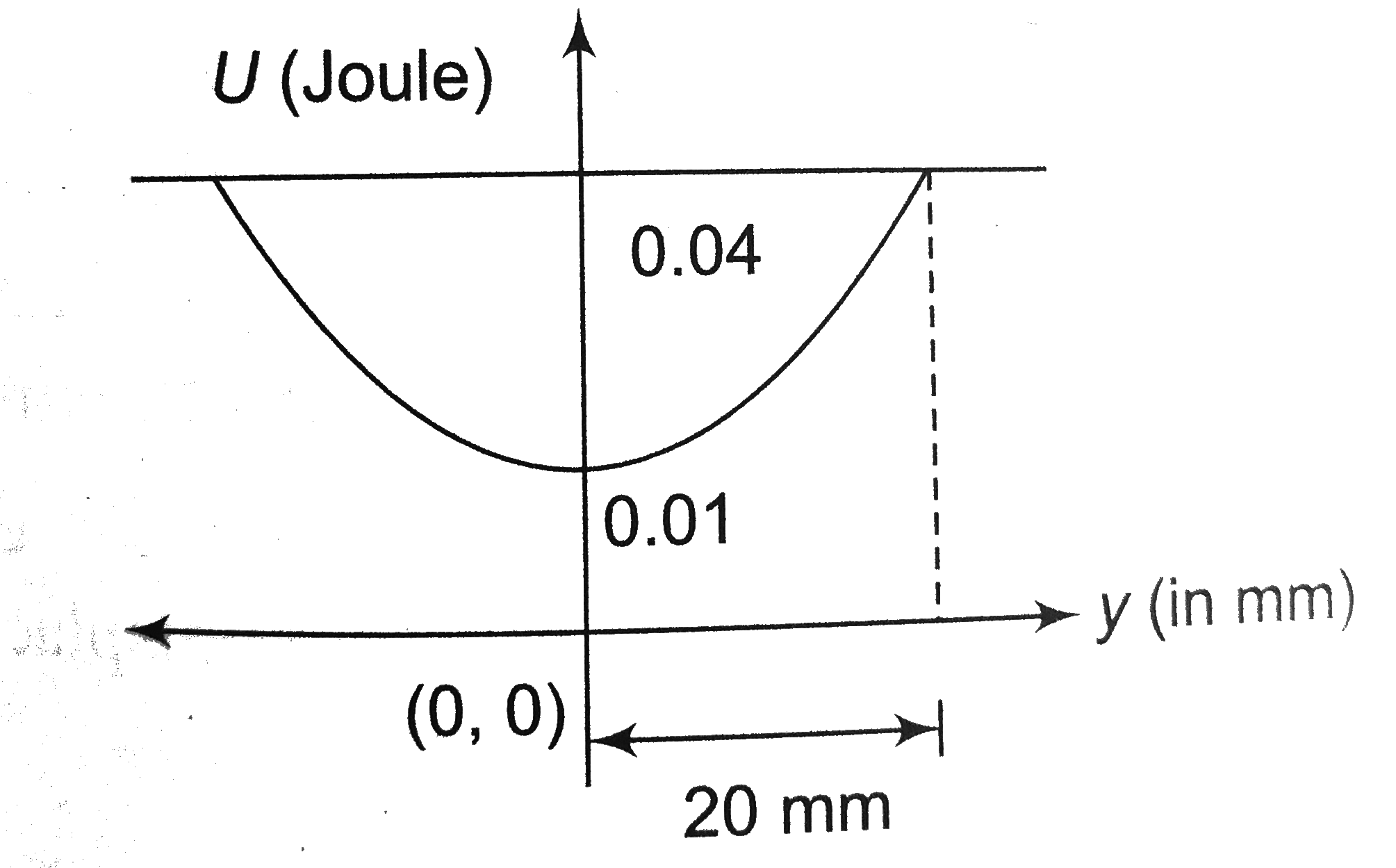 A1×102N/mB150N/mC0.667×102N/mD3×102N/m
A1×102N/mB150N/mC0.667×102N/mD3×102N/mThe variation of potenial energy of harmoic oscillartor is as show in figure . The spring constant is
 A1×102N/mB150N/mC0.667×102N/mD3×102N/m
A1×102N/mB150N/mC0.667×102N/mD3×102N/mThe variation of the potential energy of harmonic oscillator is as shown in the figure. The spring constant is
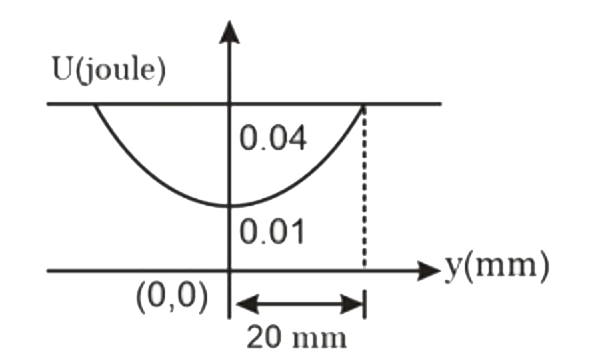 A1×102Nm−1B150Nm−1C66.7Nm−1D3×102Nm−1
A1×102Nm−1B150Nm−1C66.7Nm−1D3×102Nm−1
The variation of displacement with time of a particle executing free simple harmonic motion is shown in the figure.
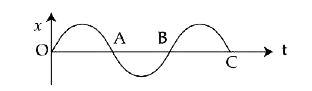
The potential energy U(x) versus time (t) plot of the particle is correctly shown in figure :
View SolutionThe variation of potential energy (U) of a simple harmonic oscillator is as shown. Then force constant of the system is (PE is in joules, displacement 'x' is in mm)
View SolutionThe pointer reading versus load graph for a spring balance is as shown in the figure.
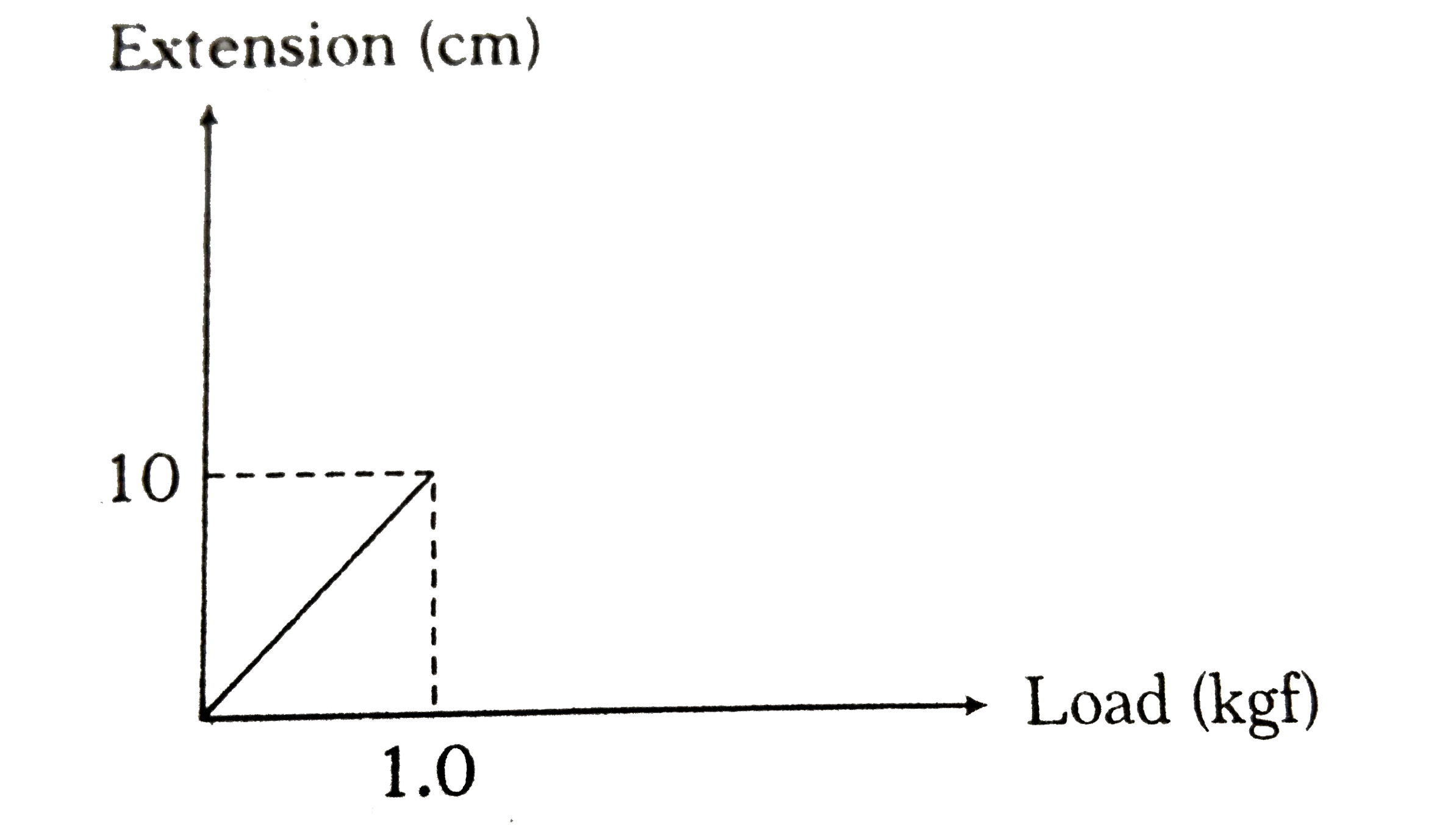
The spring constant is
View SolutionThe variations of potential energy (U) with position x for three simple harmonic oscillators A, B and C are shown in figure. The oscillators have same mass. The time period of oscillation is greatest for

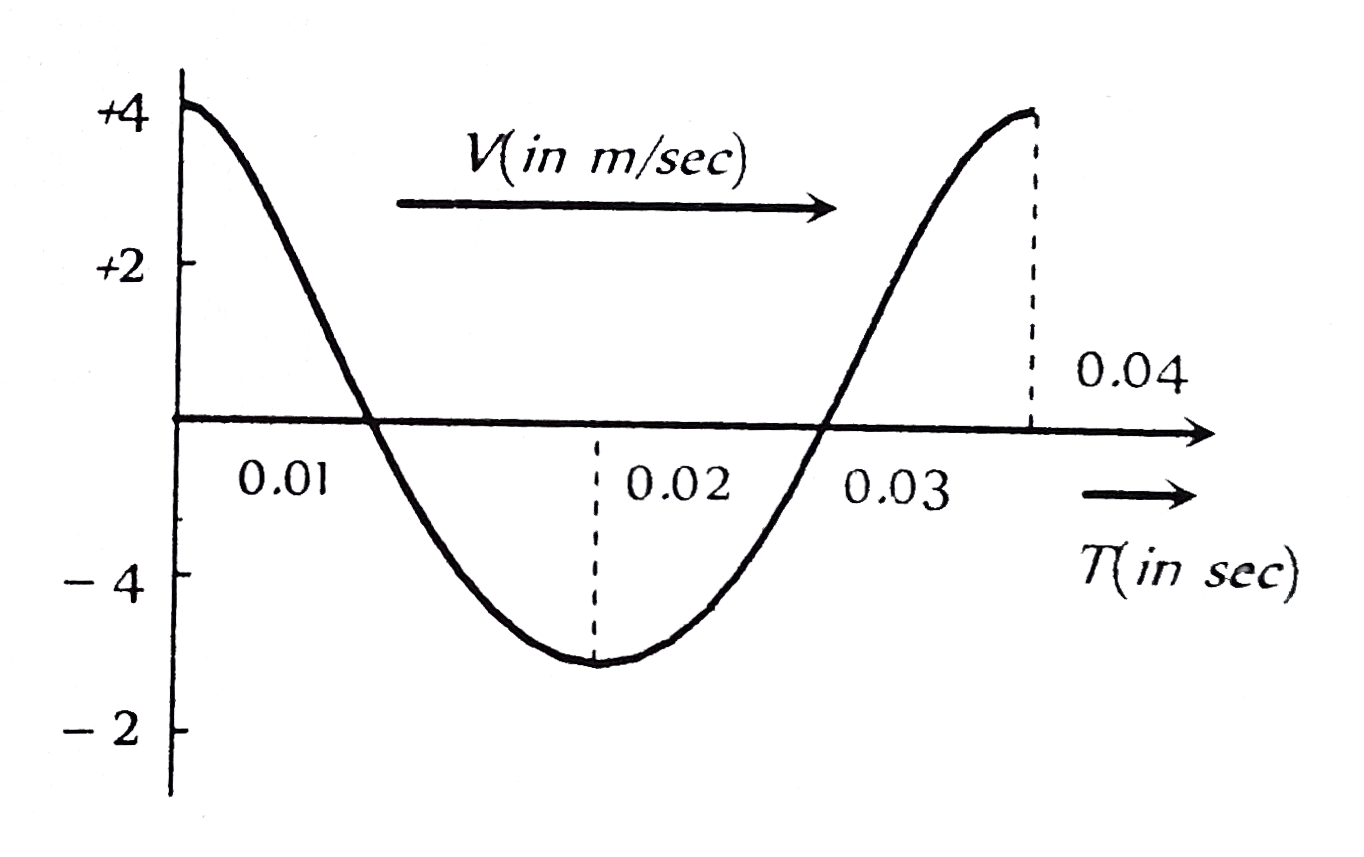
View SolutionThe velocity-time diagram of a harmonic oscillator is shown in the adjoining figure. The frequency of oscillation is
View Solution
