A uniform rod of density is placed in a wide tank containing a liquid of density . The depth of liquid in the tank is half the length of the rod. The rod is in equilibrium, with its lower end resting on the bottom of the tank. In this position the rod makes an angle with the horizontal.
The correct Answer is:A
Force of buoyancy-
(l=PR)
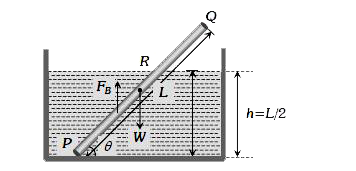
For rotational equilibrium-
.
Topper's Solved these Questions
- FLUID MECHANICSBOOK - ERRORLESSCHAPTER - FLUID MECHANICSEXERCISE - PAST YEARS QUESTIONS
14 Videos
- FLUID MECHANICSBOOK - ERRORLESSCHAPTER - FLUID MECHANICSEXERCISE - ASSERTION AND REASON
23 Videos
- FLUID MECHANICSBOOK - ERRORLESSCHAPTER - FLUID MECHANICSEXERCISE - NCERT BASED QUESTIONS(PASCAL.S LAW AND ARCHIMEDES PRINCIPLE)
23 Videos
- ELASTICITYBOOK - ERRORLESSCHAPTER - ELASTICITYEXERCISE - ASSERTION & REASON
10 Videos
- FRICTION BOOK - ERRORLESSCHAPTER - FRICTION EXERCISE - ASSERTION & REASON
8 Videos
Similar Questions
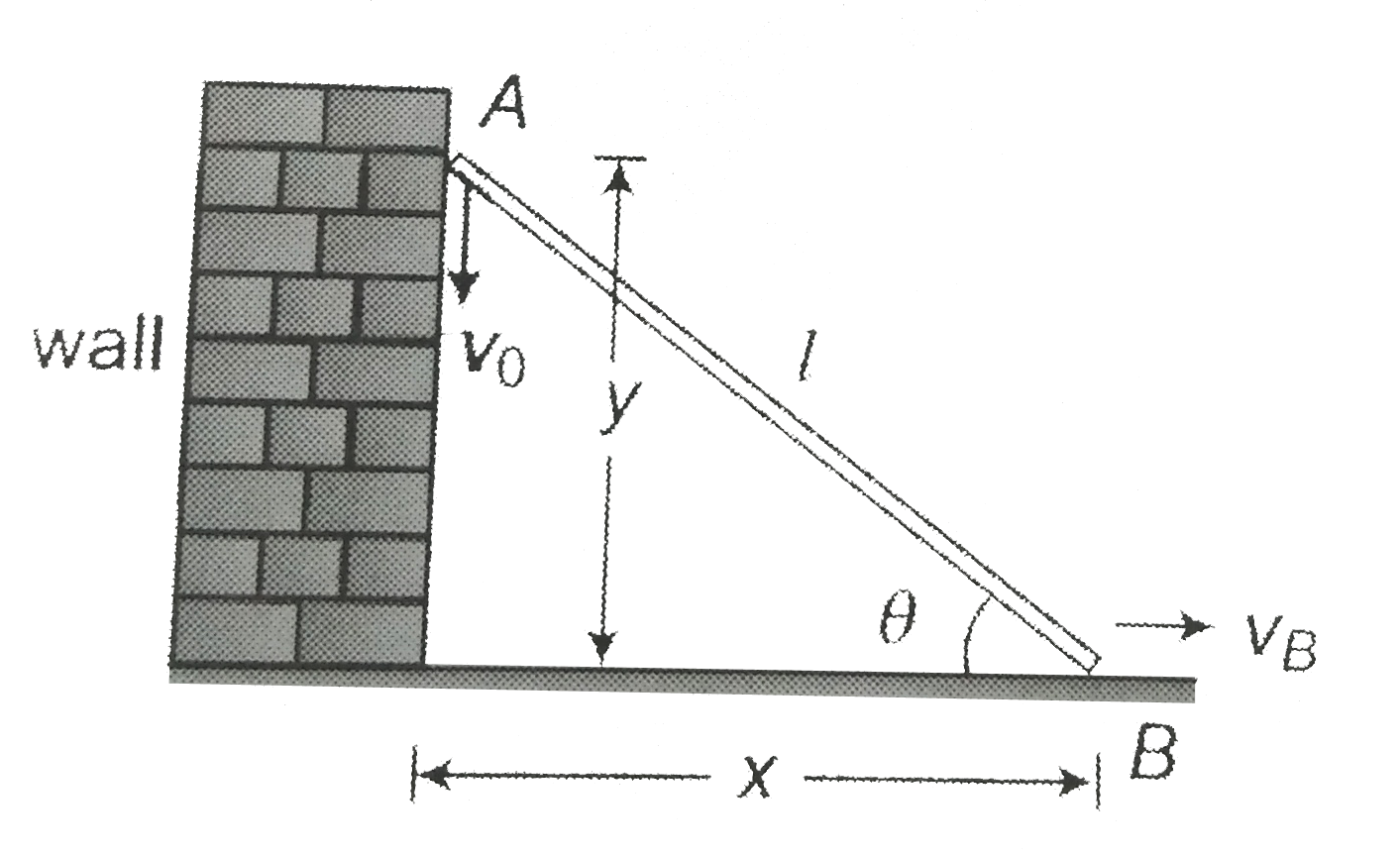
Consider a rod of length l resting on a wall and the floor. If the velocity of the upper end of a rod A is v0 in downward direction, find the velocity of the lower end B at this iinstant, when the rod makes an angle θ with horizontal
View SolutionA body of density ρ is released gently on the surface of a layer of liquid of depth d and density ρ'(ρ'<ρ) . Show that it will reach the bottom of the liquid after a time.
[2dρg(ρ−ρ')]1/2 .
View Solution
Knowledge Check
A beaker containing a liquid of density ρ moves up with an acceleration a. The pressure due to the liquid at a depth h below the free surface of the liquid is.
AhρgBhρ(g+a)Chρ(g−a)D2hρg(g−ag+a)
A sealed tank containing a liquid of density ρ moves with a horizontal acceleration a, as shown in the figure. The difference in pressure between the points A and B isAhρgBlρaChρg−lρaDhρg+lρaA sealed tank containing a liquid of density ρ moves with horizontal acceleration a as shown in the figure. The difference in pressure between two points A and B will be
 AhρgBlρgChρg−lρaDhρg−lρa
AhρgBlρgChρg−lρaDhρg−lρa
A liquid of density ρ0 is filled in a wide tank to a height h. A solid rod of length L, cross-section A and density ρ is suspended freely in the tank. The lower end of the rod touches the base of the tank and h=L/n (where n gt 1). Then the angle of inclination θ of the rod with the horizontal in equilibrium position is
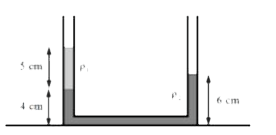
View SolutionA narrow U-tube placed on a horizontal surface contains two liquids of densities ρ1 and ρ2 . The columns of the liquids are indicated in the figure. The ratio ρ1ρ2 is equal to :
View SolutionA uniform rod of length L pivoted at the bottom of a pond of depth L/2 stays in stable equilibrium as shown in the figure.

Find the angle 0 if the density of the material of the rod is half of the density of water.
View SolutionA trolley containing a liquid slides down a smooth inclined plane of angle α with the horizontal. Find the angle of inclination θ of the free surface with the horizontal.

View SolutionThere are two holes, each of cross-sectional area a, on the oppisite side of a wide rectangular tank containing a liquid of density ρ. When the liquid flows out of the holes the net force on the tank is [h is the vertical distance between the two holes].
View Solution
