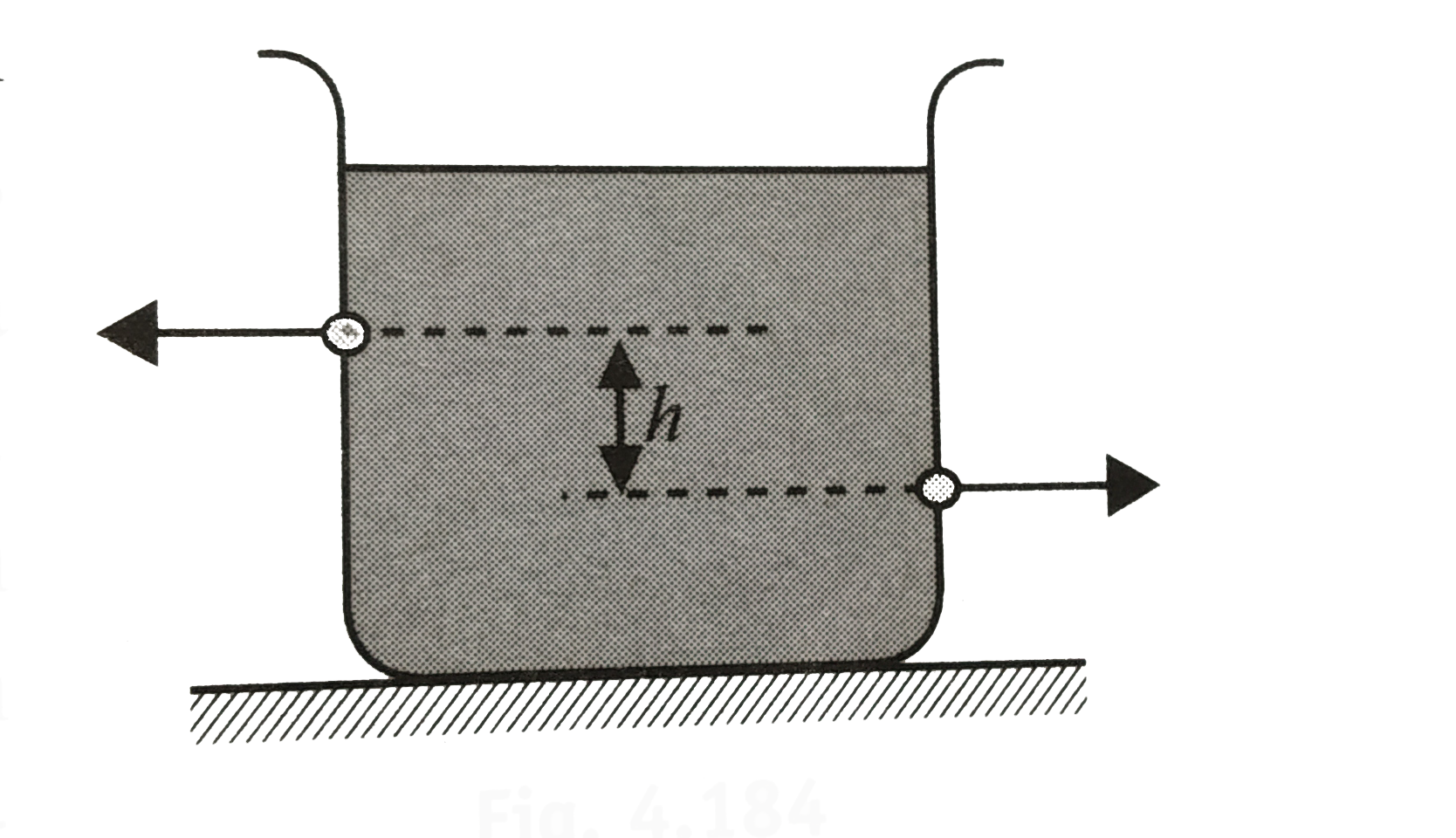
There are two identical small holes of area of cross section a on the opposite sides of a tank containing liquid of density ρ. The differences in height between the holes is h. The tank is resting on a smooth horizontal surface. The horizontal force which will have to be applied on the tank to keep it in equilibrium is
ghρa
2gh/ρa
2ρagh
ρgh/a
The correct Answer is:C
Net force on container -
F=FB−FA=dpBdt−dpAdt
=avBρ×vB−avAρ×vA
aρ(v2B−v2A)
According Bernoulli.s Principle -
PA+12ρv2A−ρgh=PB+12ρv2B
⇒v2B−v2A=2gh
∴F=−aρ×2gh=−2aρgh
(Neglect -ve sign it shows direction only).
Topper's Solved these Questions
- FLUID MECHANICSBOOK - ERRORLESSCHAPTER - FLUID MECHANICSEXERCISE - PAST YEARS QUESTIONS
14 Videos
- FLUID MECHANICSBOOK - ERRORLESSCHAPTER - FLUID MECHANICSEXERCISE - ASSERTION AND REASON
23 Videos
- FLUID MECHANICSBOOK - ERRORLESSCHAPTER - FLUID MECHANICSEXERCISE - NCERT BASED QUESTIONS(PASCAL.S LAW AND ARCHIMEDES PRINCIPLE)
23 Videos
- ELASTICITYBOOK - ERRORLESSCHAPTER - ELASTICITYEXERCISE - ASSERTION & REASON
10 Videos
- FRICTION BOOK - ERRORLESSCHAPTER - FRICTION EXERCISE - ASSERTION & REASON
8 Videos
Similar Questions
There are two holes, each of cross-sectional area a, on the opposite side of a wide rectangular tank containing a liquid of densityρ. When the liquid flows out of the holes, find the net force on the tank. Given h is the vertical distance between two holes.
View SolutionA tank of square cross-section of each side is filled with a liquid of height h . Find the thrust experienced by the vertical surfaces and bottom surface of the tank.
View Solution
Knowledge Check
There are two identical small holes of area of cross section a on the opposite sides of a tank containing liquid of density ρ. The differences in height between the holes is h. The tank is resting ona smooth horizontal surface. The horizontal force which will have to be applied on the tank to keep it inequilibrium is
 AghρaB2ghρaC2ρaghDρgha
AghρaB2ghρaC2ρaghDρghaThere are two identical small holes on the opposite sides of a tank containing a liquid. The tank is open at the top. The difference in height between the two holes is h. As the liquid comes out of the two holes. The tank will experience a net horizontal force proportional to.
 .A√hBhCh3/2Dh2
.A√hBhCh3/2Dh2There are two holes, each of cross-sectional area a, on the oppisite side of a wide rectangular tank containing a liquid of density ρ. When the liquid flows out of the holes the net force on the tank is [h is the vertical distance between the two holes].
A2αρghB4αρghC0.5αρghDαρgh
On the opposite sides of vertical vessel filled with water, two identical holes are opened. If area of cross-section for each is a and difference of height of these two is h and p is density of water, then force on the vessel is
View Solution
A sealed tank containing a liquid of density ρ moves with a horizontal acceleration a, as shown in the figure. The difference in pressure between the points A and B is
View SolutionA sealed tank containing a liquid of density ρ moves with horizontal acceleration a as shown in the figure. The difference in pressure between two points A and B will be

View SolutionA cylindrical tank having cross - sectional area A=0.5m2 is filled with two liquids of density ρ1=900 kg m−3andρ2=600 kg m−3 , to a height a =6cm2 is made in right vertical wall at a height y = 20 cm from the bottom . A horizontal force F is applied on the tank to keep it in static equilibrium . The tank is lying on a horizontal surfaces . Neglect mass of cylindrical tank camparison to mass of liquids ( take g=10ms−2)
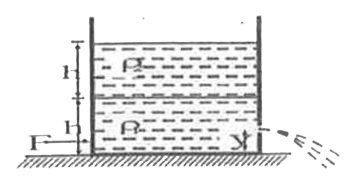
Minimum and maximum values of F to keep the cylinder in static just after the water starts to spill through the hole . If the co - efficient of static friction between contact surfaces is 0.01
View SolutionA container of large uniform cross-sectional area A resting on a horizontal surface, holes two immiscible, non-viscon and incompressible liquids of densities d and 2d each of height H/2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P0. A homogeneous solid cylinder of length L(L<H/2) and cross-sectional area A/5 is immeresed such that it floats with its axis vertical at the liquid-liquid interface with length L/4 in the denser liquid,

The cylinder is then removed and the original arrangement is restroed. a tiny hole of area s(s<<A) is punched on the vertical side of the container at a height h(h<H/2). As a result of this, liquid starts flowing out of the hole with a range x on the horizontal surface.
The total pressure with cylinder, at the bottom of the container is
View Solution
