A long solenoid of diameter 0.1m has 2×104 turns per metre. At the centre of the solenoid, a coil of 100 turns and radius 0.01m is placed with its axis coinciding with the solenoid axis. The current in the solenoid reduces at a constant rate to 0A from 4A in 0.05 .If the resistance of the coil is 10π2ohm, the total charge (in μC ) flowing through the coil during this time is
32πμC
16μC
32μC
16πμC
The correct Answer is:C
q=ΔφR=μ0n(i−0)NAR
N = Number of loops in coil
A = Area of coil having radius 0.01 m
n = Number of turns per unit length of solenoid
Q=4π×10−7×2×104×4×100×π×10−410π2=32μC.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - ERRORLESSCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - ASSERTION & REASON
20 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - ERRORLESSCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - NCERT BASED QUESTIONS (APPLICATION OF EMI (Dynamo, Transformer…))
20 Videos
- CURRENT ELECTRICITYBOOK - ERRORLESSCHAPTER - CURRENT ELECTRICITYEXERCISE - ASSERTION AND REASON
26 Videos
- ELECTRON, PHOTON, PHOTOELECTRIC EFFECT & X -RAYBOOK - ERRORLESSCHAPTER - ELECTRON, PHOTON, PHOTOELECTRIC EFFECT & X -RAYEXERCISE - ASSERTION & REASON
27 Videos
Similar Questions
A long solenoid of diameter 0.1 m has 2×104 turns per meter. At centre of the solenoid is 100 turns coil of radius 0.01 m placed with its axis coinciding with solenoid axis. The current in the solenoid is decreased at a constant rate form + 2 A to - 2 A in 0.05 s. Find the e.m.f. induced in the coil. Also, find the total charge flowing through the coil during this time, when the resistance of the coil is 10π2ohm.
View SolutionA long solenoid of diameter 0.1m has 2×104 turns per metre. At the centre of the solenoid, a 100−turns coil of radius 0.01m is placed with its axis coinciding with the constant rate from +2A to 2A in 0.05s. Find the total charge (in μC) flowing through the coil during this time when the resistance of the coil is 40≠2Ω.
View Solution
Knowledge Check
A long solenoid of diameter 0.1 m has 2×104 turns per meter. At centre of the solenoid is 100 turns coil of radius 0.01 m placed with its axis coinciding with solenoid axis. The current in the solenoid reduce at a constant rate to 0A from 4 a in 0.05 s . If the resistance of the coil is 10π2Ω, the total charge flowing through the coil during this time is
A16μCB32μCC15πμCD32πμCA long solenoid of diameter 0.1 m has 2×104 turns per meter. At centre of the solenoid is 100 turns coil of radius 0.01 m placed with its axis coinciding with solenoid axis. The current in the solenoid reduce at a constant rate to 0A from 4 a in 0.05 s . If the resistance of the coil is 10π2Ω, the total charge flowing through the coil during this time is
A32πμCB16μCC32μCD16πμCAn ideal solenoid of cross-sectional area 10−4m2 has 500 turns per metre. At the centre of this solenoid, another coil of 100 turns is wrapped closely around it. If the current in the coil changes from 0 to 2 A in 3.14 ms, the emf developed in the second coil is
A1 mvB2 mvC3 mvD4 mv
A long solenoid with 1.5 turns per cm has a small loop of area 2.0cm2 placed inside the solenoid normal to its axis. If the current in the solenoid changes steadily from 2.0A to 4.0A in 1.0s. The emf induced in the loop is
View SolutionThrough a long solenoid of diameter 4.1 cm, having 100 turns per cm, a current I = 1A is flowing. At its centre, a 60 turns closely packed coil of diameter 3.1 cm si placed such that the coil is coaxial with the long solenoid. The current in the solenoid is reduced to zero at a steady rate in 10 ms. What is the magnitude of emf induced in the coil while the current in the solenoid is changing?
View SolutionA current l = 1.5 A is flowing through a long solenoid of diameter 3.2 cm, having 220 turns per cm. At its centre, a 130 turn closely packed coil of diameter 2.1 cm is placed such that the coil is coaxial with the long solenoid. The current in the solenoid is reduced to zero at a steady rate in 25 ms. What is the magnitude of emf induced in the coil while the current in the solenoid is changing?
View SolutionA 0.100 m long solenoid has a radius of 0.050 m and 1.50×104 turns. The current in the solenoid changes at a rate of 6.0 A/s. A conducting loop of radius 0.0200 m is placed at the center of the solenoid with its axis the same as that of the solenoid as shown.
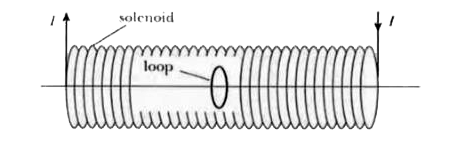
Determine the mutual inductance of this combination.
View SolutionA 0.100 m long solenoid has a radius of 0.050 m and 1.50×104 turns. The current in the solenoid changes at a rate of 6.0 A/s. A conducting loop of radius 0.0200 m is placed at the center of the solenoid with its axis the same as that of the solenoid as shown.
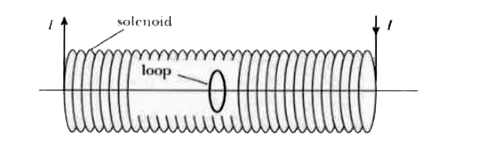
Determine the induced emf in the loop.
View Solution
