A conducting square frame of side 'a' and a long straight wire carrying current I are located in the same plane as shown in the figure. The frame moves to the right with a constant velocity 'V'. The emf induced in the frame will be proportional to
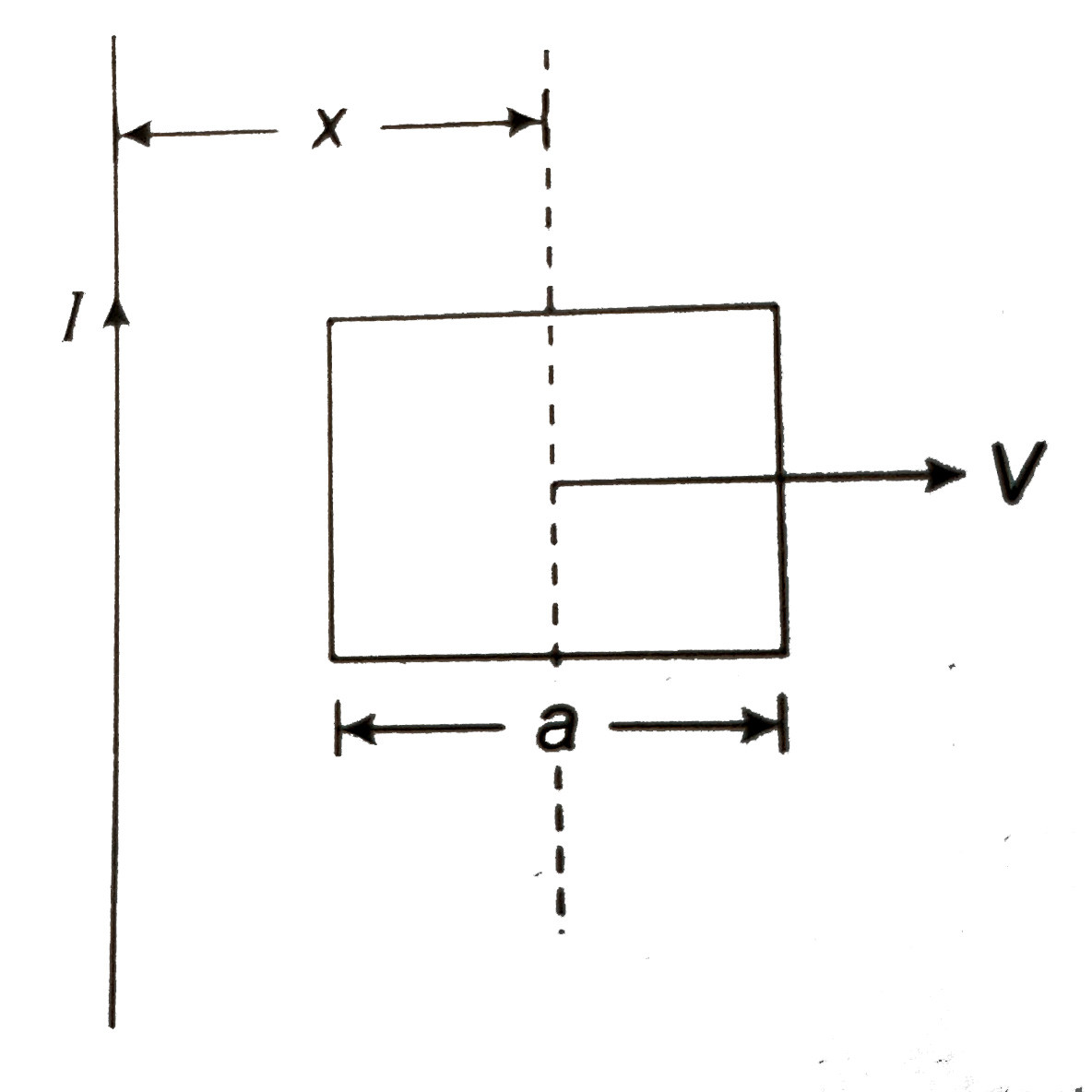
1(2x−a)2
1(2x+a)2
1(2x−a)(2x+a)
1/x2
The correct Answer is:C
emf in PQ -
e1=B1av=μ0I2π(χ−a2)av
emf in RS-
e2=B2av=μ0I2π(χ+a2)av
enet=e1−e2=μ0Iav2π⎡⎢
⎢⎣1(χ−a2)−1(χ+a2)⎤⎥
⎥⎦
enet∝1(2χ−a)(2χ+a).

Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - ERRORLESSCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - ASSERTION & REASON
20 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - ERRORLESSCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - NCERT BASED QUESTIONS (APPLICATION OF EMI (Dynamo, Transformer…))
20 Videos
- CURRENT ELECTRICITYBOOK - ERRORLESSCHAPTER - CURRENT ELECTRICITYEXERCISE - ASSERTION AND REASON
26 Videos
- ELECTRON, PHOTON, PHOTOELECTRIC EFFECT & X -RAYBOOK - ERRORLESSCHAPTER - ELECTRON, PHOTON, PHOTOELECTRIC EFFECT & X -RAYEXERCISE - ASSERTION & REASON
27 Videos
Similar Questions
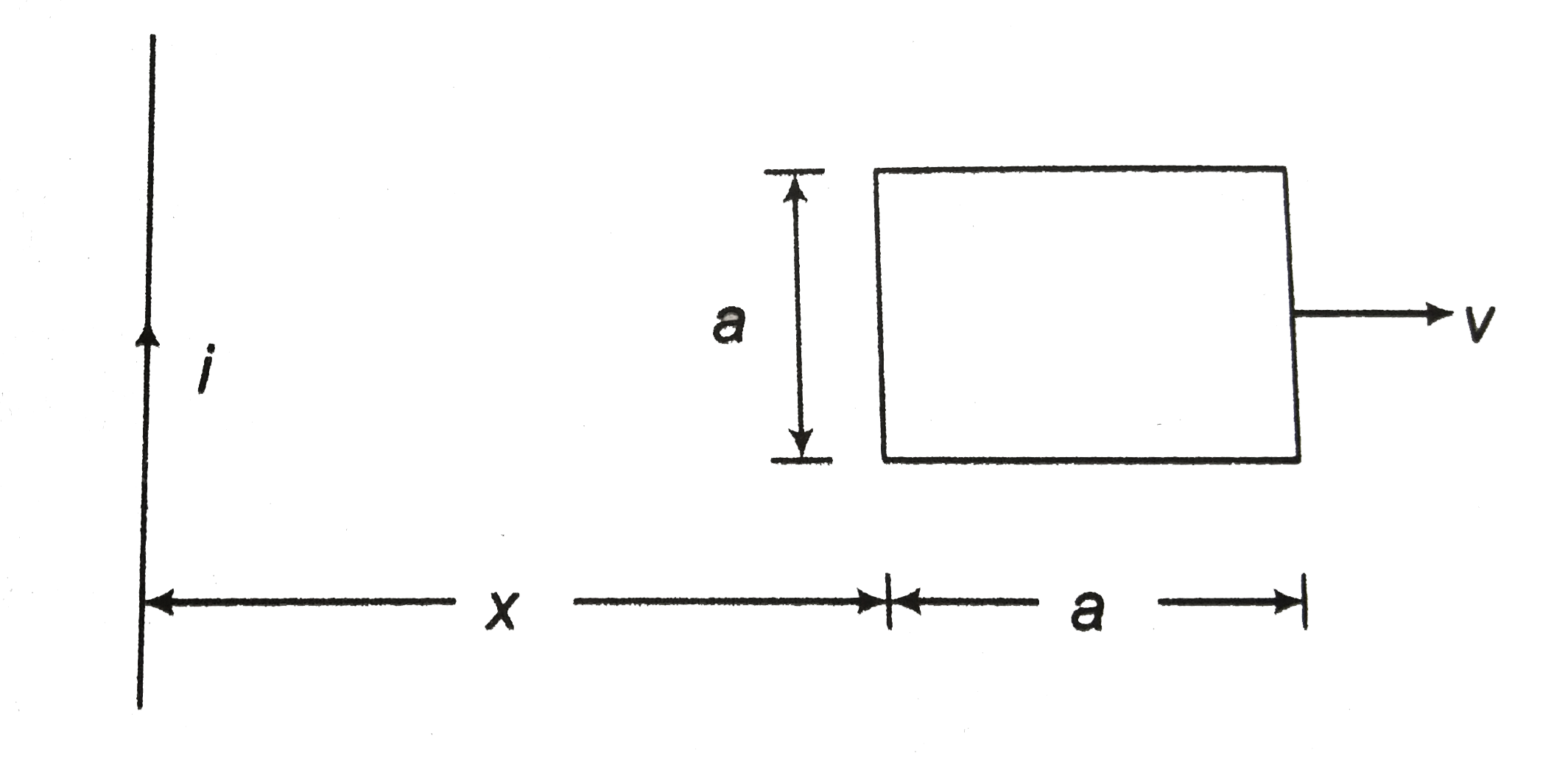
A square frame with side a and a long straight wire carrying a current i are located in the same plane as m shown in figure. The fram translates to the right with a constant velocity v. Find the emf induced in the frame as a function of distance x.
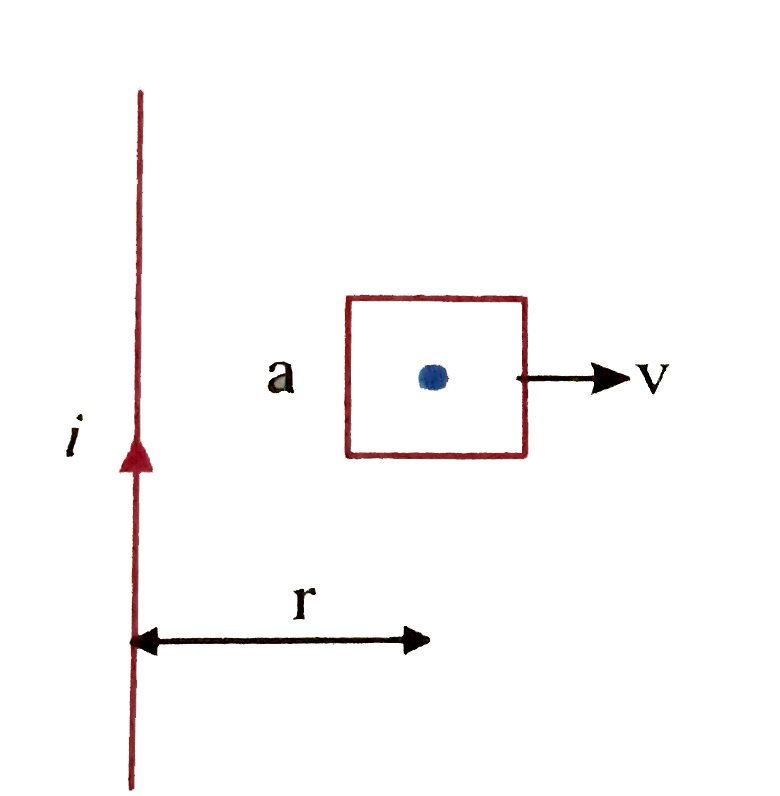
View SolutionA square loop of side a is placed in the same plane as a long straight wire carrying a current i. The centre of the loop is at a distance r from wire where r>>a. The loop is moved away from the wire with a constant velocity v. The induced e.m.f in the loop is
View Solution
Knowledge Check
The field due to a long straight wire carrying a current I is proportional to
AIB√ICI2D1/IA field due to a long straight wire carrying a current I is proportional to
AlBl2Cl3D√lThe field due to a long straight wire carrying a current I is proportional to
AlBI3C√ID1I
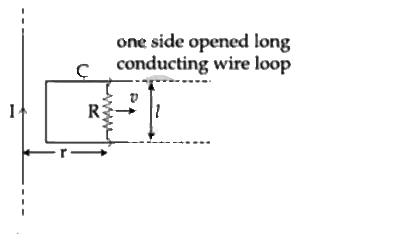
An infinitely long straight wire carrying current I , one side opened rectangular loop and a conductor C with a sliding connector are located in the same plane , as shown in the figure. The connector has length l and resistance R . It slides of the right with a velocity v. The resistance of the conductor and the self inductance of the loop are negligible . The induced current in the loop , as function of separation r between the conductor and the straight wire is :
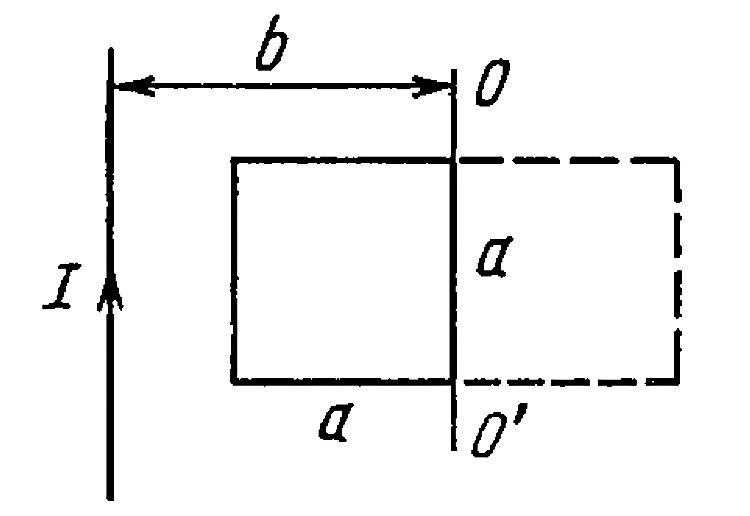
View SolutionA square wire frame with side a and a straight conductor carrying constant current I are located in the same plane (Fig). The inductance and the resitance of the frame are equal to L and R respectively. The frame was turned throgh 180∘ about the axis OO'separated fromt the current carrying conductor by a distance b. FInd the electric charge having flown through the frame.
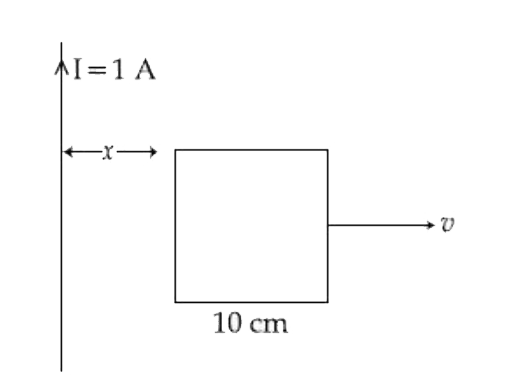
View SolutionA square frame of side 10 cm and a long straight wire carrying current 1 A are in the plane of the paper. Starting from close to the wire, the frame moves towards the right with a constant speed of 10ms−1 (sec figure). The e.m.f induced at the time the left arm of the frame is at x = 10 cm from the wire is
View SolutionThe field due to a long straight wire carrying a current I is proportional to
View SolutionA square frame with side 'a' and a straight conductor carrying a constant current I are located in the same plane. The resistance of the frame is equal to R. The frame was turned through 180∘ about the axis OO' separated from the current-carrying conductor by a distance b=2a. If the electric charge that flowed through the frame be expressed as a function of a,I,R it takes the form q=constant ×am×In×Rp. Find m+n+p.
View Solution
