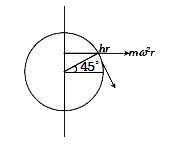
A plank is resting on a horizontal ground in the northern hemisphere of the Earth at a latitude. Let the angular speed of the Earth be and its radius . The magnitude of the frictional force on the plank will be
Zero
The correct Answer is:C
where
Topper's Solved these Questions
- GRAVITATIONBOOK - ERRORLESSCHAPTER - GRAVITATIONEXERCISE - NCERT BASED QUESTIONS (Gravitation Potential, Energy and Escape Velocity)
38 Videos
- GRAVITATIONBOOK - ERRORLESSCHAPTER - GRAVITATIONEXERCISE - NCERT BASED QUESTIONS (Motion of Satellite)
46 Videos
- GRAVITATIONBOOK - ERRORLESSCHAPTER - GRAVITATIONEXERCISE - Assertion and Reason
25 Videos
- FRICTION BOOK - ERRORLESSCHAPTER - FRICTION EXERCISE - ASSERTION & REASON
8 Videos
- KINETIC THEORY OF GASES BOOK - ERRORLESSCHAPTER - KINETIC THEORY OF GASES EXERCISE - ASSERTION AND REASON
16 Videos
Similar Questions
In the figure shown, a solid sphere of mass 'm' and radius r is released from a height 6r to slide down a smooth surface. A plank of same mass 'm' touches the horizontal portion of the surface at the ground. The co-efficient of friction between the plank and the sphere is μ and that between the plank and the ground is μ/4. Find the work done by the friction force between the plank and the ground till the sphere starts pure rolling on the plank. Neglect the height of the plank.

View Solution
A horizontal plank having mass m lies on a smooth horizontal surface. A sphere of same mass and radius r is spined to angular frequency ω0 and gently placed on the plank as shown in the figure. If coefficient of friction between the plank and the sphere is μ. Find the distance moved by the plank till sphere starts pure rolling on the plank. the plank is long enough.
View Solution
Knowledge Check
A uniform thin rod of mass m and length R is placed normally on surface of earth as shown. The mass of earth is M and its radius R. Then the magnitude of gravitational force exerted by earth on the rod is
 AGMm2R2BGMm4R2C4GMm9R2DGMm8R2
AGMm2R2BGMm4R2C4GMm9R2DGMm8R2A train of mass m moves with a velocity υ on the equator from east to west. If ω is the angular speed of earth about its axis and R is the radius of the earth then the normal reaction acting on the train is
Amg[1−(ωR−2υ)ωg−υ2Rg]Bmg[1−2(ωR−υ)ωg−υ2Rg]Cmg[1−(ωR−2υ)ωg−υ2Rg]Dmg[1−2(ωR−υ)ωg−υ2Rg]If ωE and ωH are the angular velocities of the earth rotating about its own axis and the hour hand of the clock respectively, then
AωE=15ωHBωE=2ωHCωE=ωHDωE=12ωH
A plank of mass M rests on a smooth horizontal plane. A sphere of mass m and radius r is placed on the rough upper surface of the plank and the plank is suddenly given a velocity v in the direction of its length. Find the time after which the sphere begins pure rolling, if the coefficient of friction between the plank and the sphere is μ and the plank is sufficiently long.
View SolutionIf earth suddenly stop rotating , then the weight of an object of mass m at equator will [ ω is angular speed of earth and R is its radius . ]
View SolutionA long horizontal plank of mass m is lying on a smooth horizontal surface. A sphere of same mass m and radius r is spinned about its own axis with angular velocity we and gently placed on the plank. The coefficient of friction between the plank and the sphere is μ. After some time the pure rolling of the sphere on the plank will start. Answer the following questions.

Find the displacement of the plank till the sphere starts pure rolling.
View SolutionA long horizontal plank of mass m is lying on a smooth horizontal surface. A sphere of same mass m and radius r is spinned about its own axis with angular velocity we and gently placed on the plank. The coefficient of friction between the plank and the sphere is μ. After some time the pure rolling of the sphere on the plank will start. Answer the following questions.
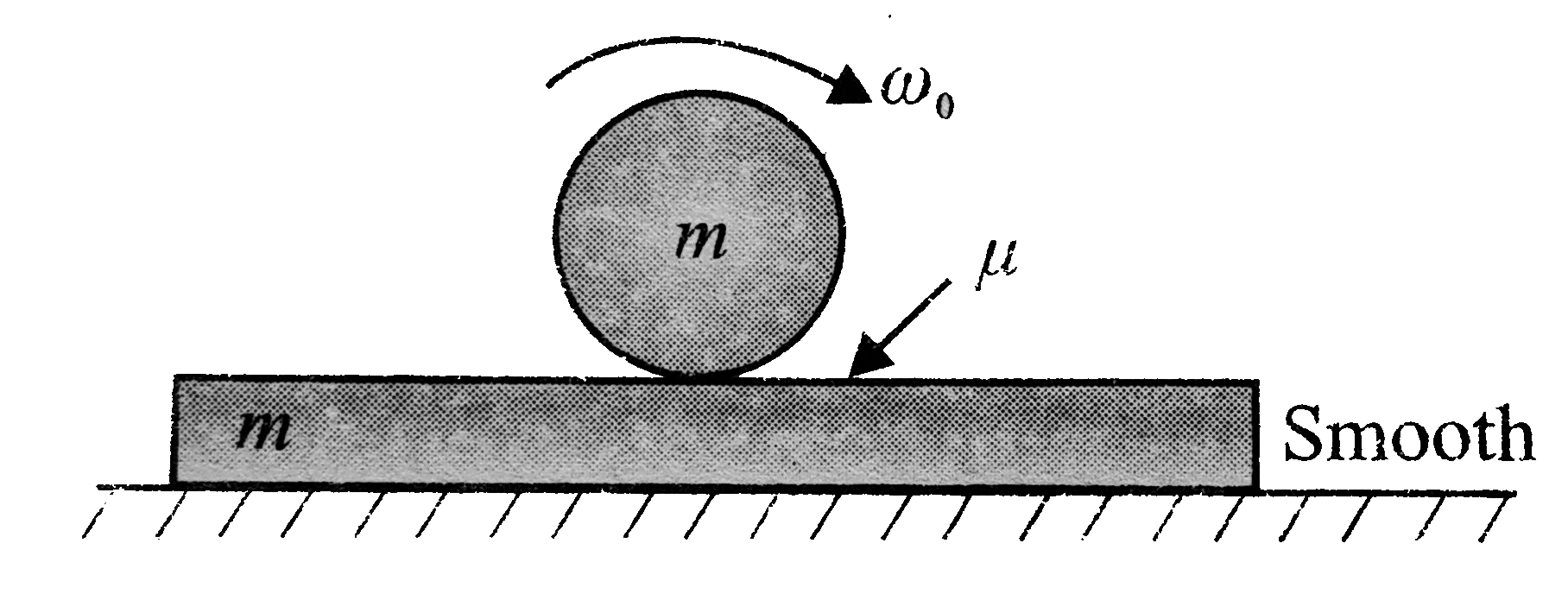
Find the time t at which the pure roiling starts
View SolutionA long horizontal plank of mass m is lying on a smooth horizontal surface. A sphere of same mass m and radius r is spinned about its own axis with angular velocity we and gently placed on the plank. The coefficient of friction between the plank and the sphere is μ. After some time the pure rolling of the sphere on the plank will start. Answer the following questions.

Find the velocity of the sphere after the pure rolling starts
View Solution
