One mole of an ideal diatomic gas undergoes a transition from A to B along a path AB as shown in the figure,

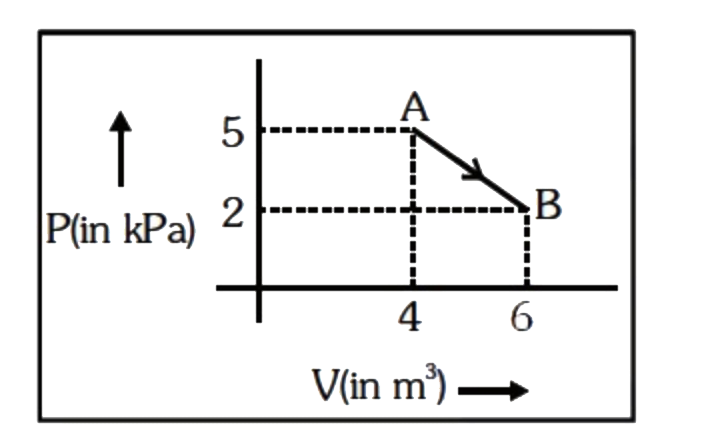
The change in internal energy of the gas during the transition is :

A

$- 20 k J$

B

$20 J$

C

$- 12 k J$

D

$20 k J$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

$Δ U = \frac{f}{2} n R Δ T f \to$ degree of freedom
$\Rightarrow Δ U = \frac{5}{2} (P_{f} V_{f} - P_{i} V_{i})$
$= \frac{5}{2} (2 \times 10^{3} \times 6 - 5 \times 10^{3} \times 4) = - 20 k J$ .

|

Updated on:21/07/2023

Class 11 PHYSICS KINETIC THEORY OF GASES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
One mole of an ideal diatomic gas undergoes a transition from A to B along a path AB as shown in (figure). The change in internal energy of the gas during the transition is $(γ = 3 / 5)$

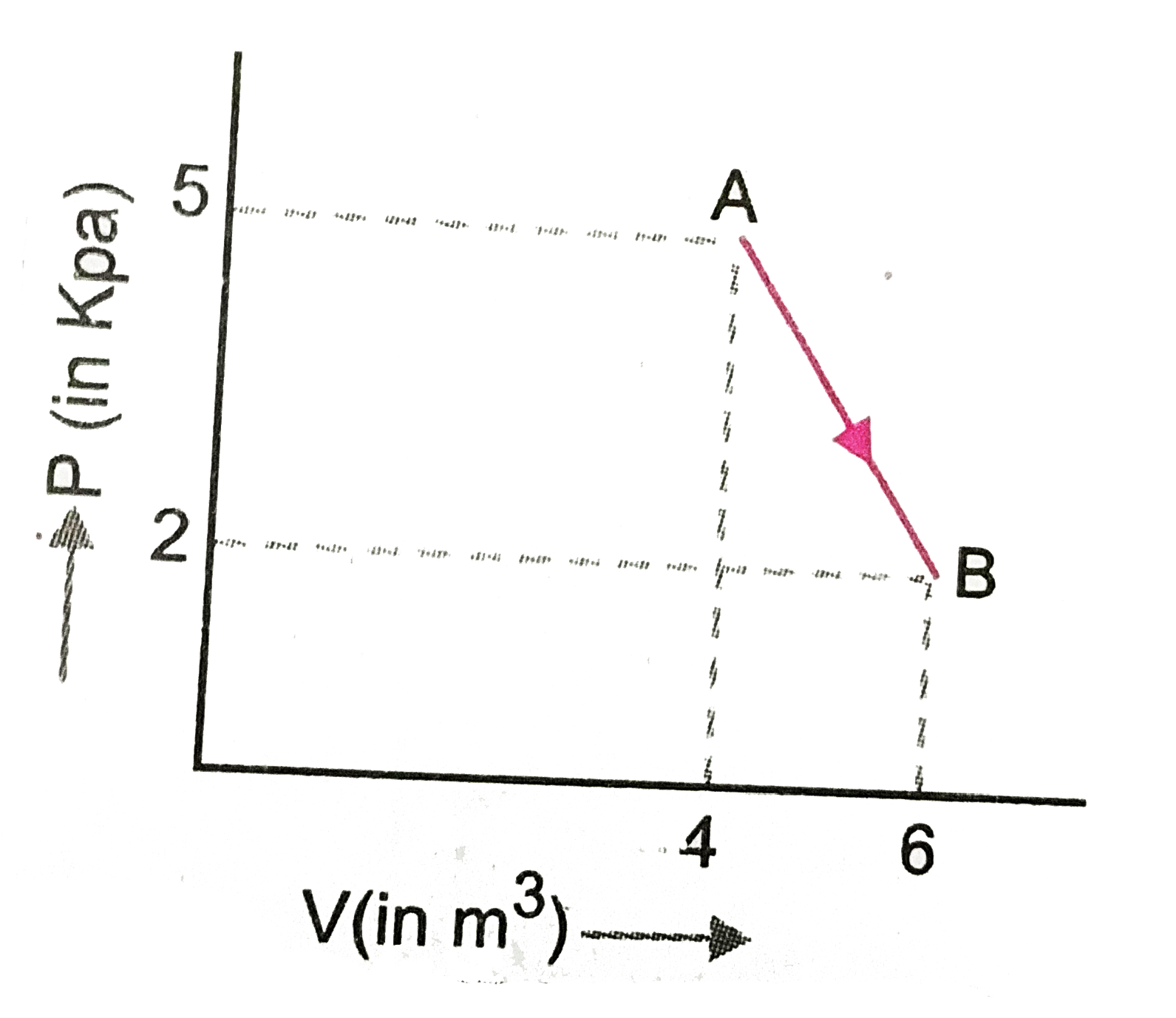A $- 20 K J$
B $20 K J$
C $- 12 K J$
D $20 K J$
Question 2 - Select One
One mole of an ideal diatomic gas undergoes a transition from A to B along a path AB as shown in (figure). The change in internal energy of the gas during the transition is $(γ = 3 / 5)$

A $- 20 K J$
B20 J
C $- 12 K J$
D20 KJ
Question 3 - Select One
A mono-atomic gas is taken along path AB as shown. Calculate change in internal energy of the gas.

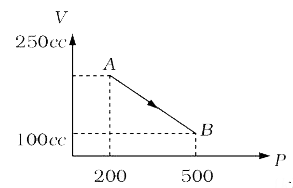A $279.8 J$
B $341 J$
C $241 J$
Dzero

ERRORLESS-KINETIC THEORY OF GASES -PAST YEARS QUESTIONS

Home
Ask Doubt
Profile