Two batteries of emf E1 and E2(E2>E1) and internal resistances r1 and r2 respectively are connected in parallel as shown in figure-
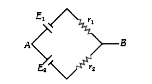
Two equivalent emf Eeq of the two cells is between E1 and E2 , i.e., E1<Eeq<E2
The equivalent emf Eeq is smaller than E1
The Eeq is given by Eeq=E1+E2 always
Eeq is independent of internal resistances r1 and r2
The correct Answer is:A
The equivalent emf of this combination is given by-
Eeq=(E2r1+E1r2r1+r2)
This suggest that the equivalent emf Eeq of the two cells is given by-
E1<Eeq<E2
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - ERRORLESSCHAPTER - CURRENT ELECTRICITYEXERCISE - NCERT BASED QUESTIONS (DIFFERENT MEASURING INSTRUMENTS)
74 Videos
- CURRENT ELECTRICITYBOOK - ERRORLESSCHAPTER - CURRENT ELECTRICITYEXERCISE - NCERT BASED QUESTIONS (HEATING EFFECT OF CURRENT)
67 Videos
- CURRENT ELECTRICITYBOOK - ERRORLESSCHAPTER - CURRENT ELECTRICITYEXERCISE - NCERT BASED QUESTIONS (Grouping of Resistances)
69 Videos
- ATOMIC AND NUCLEAR PHYSICSBOOK - ERRORLESSCHAPTER - ATOMIC AND NUCLEAR PHYSICSEXERCISE - Assertion and Reason
23 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - ERRORLESSCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - ASSERTION & REASON
20 Videos
Similar Questions
Two batteries of emf E1 and E2(E2>E1) and internal resistance r1 and r2 respectively are connected in parallel as shown in the figure. Then, which of the followings statements is correct ?
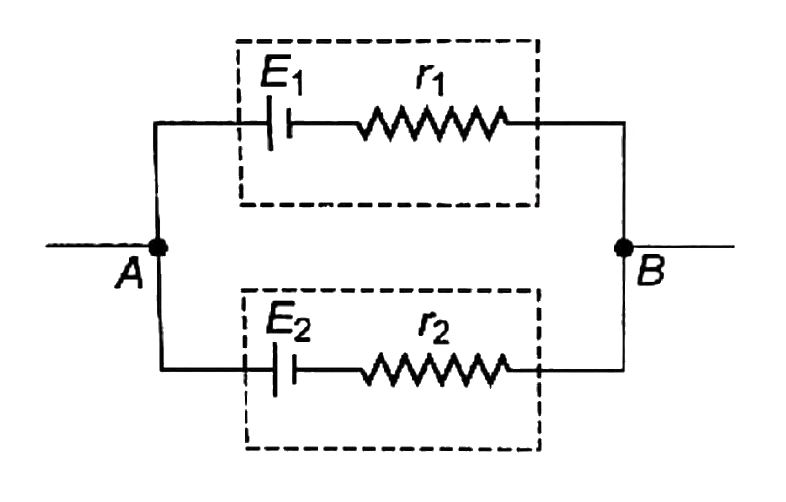
View SolutionTwo cells of emf ε1 and ε2 having internal resistances r1 and r2 respectively are connected in parallel as shown in Fig. Deduce the expressions for the equivalent emf and equivalent internal resistance of a cell which can replace the combination between the pointsB1 and B2 .

View Solution
Knowledge Check
Two batteries of emf ε1 and ε2(ε2>ε1) and internal resistances r_1 and r2 respectively are connected in parallel as shown in Fig. Then
 Athe equivalent emf εeq of the two cells is betweenε1 and ε2 i.e., ε1<εeq<ε2Bthe equivalent emf εeq is smaller than ε1Cthe εeq is given by εeq=ε1+ε2 always .Dεeq is independent of internal resistances r1 and r2
Athe equivalent emf εeq of the two cells is betweenε1 and ε2 i.e., ε1<εeq<ε2Bthe equivalent emf εeq is smaller than ε1Cthe εeq is given by εeq=ε1+ε2 always .Dεeq is independent of internal resistances r1 and r2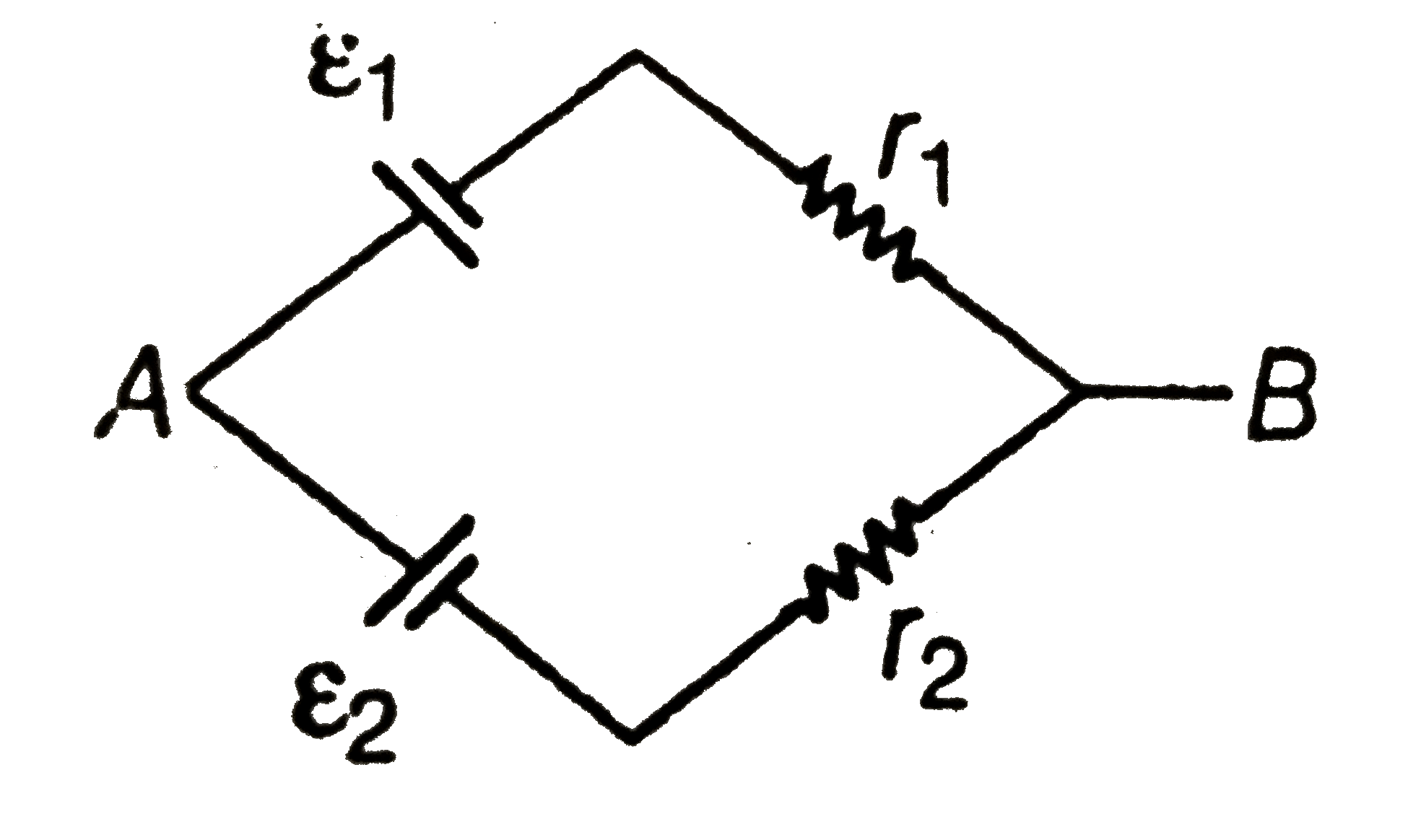
Two batteries of emf ε1andε2(ε2>ε1) and internal resistance r1andr2 respectively are connected in parallel as shown in figure.AThe equivalent emf εeq of the two cells is between ε1andε2, i.e., ε1<εeq<ε2Bthe equivalent emf εeq is smaller than ε1CThe εeq is given by εeq=ε1+ε2 always.Dεeq is independent of internal resistance r1andr2.Two batteries of emf ε1 and ε2(ε2>ε1 and internal resistances r1 and r2 respectively are connected in parallel as shown in Fig. 2 (EP).1.
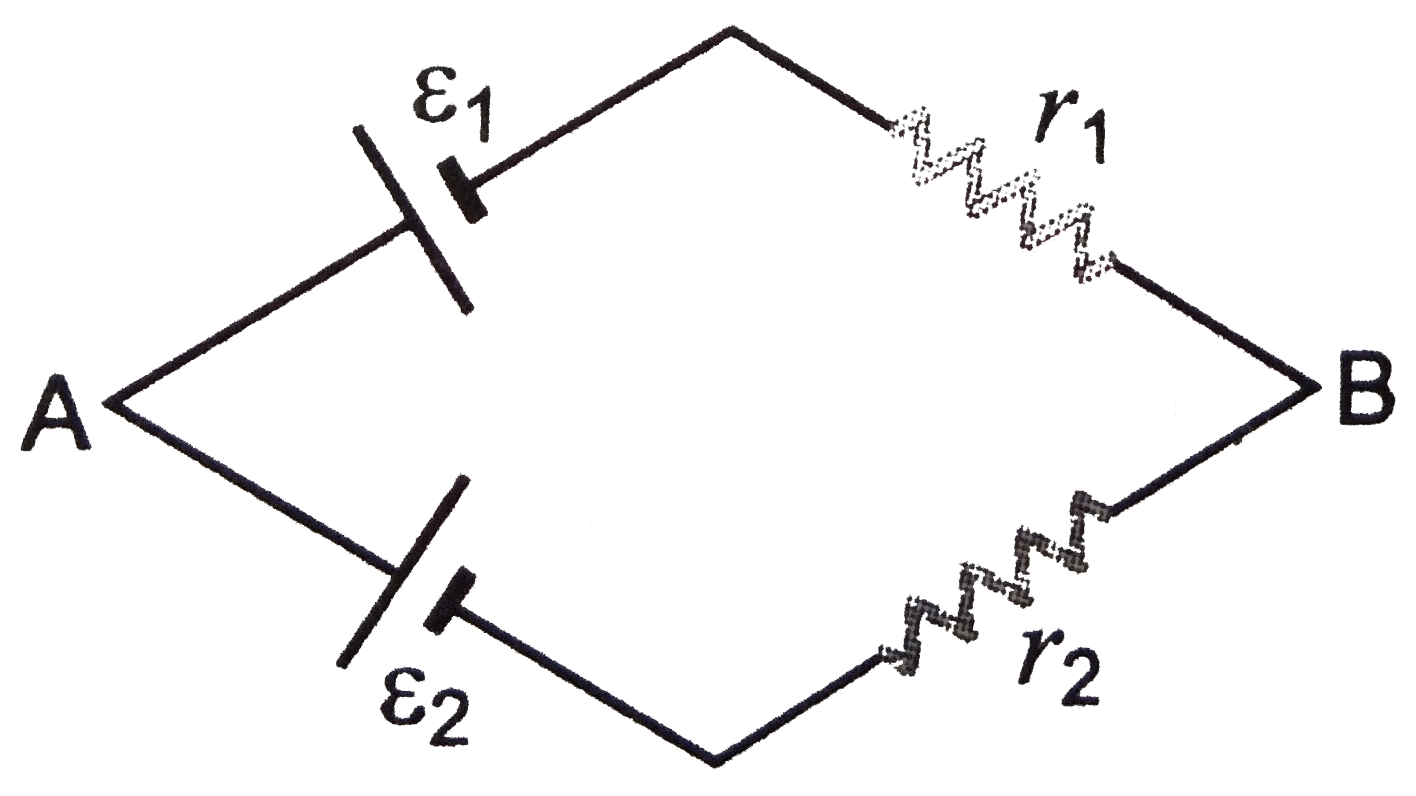 AThe equivalent emf εeq of the two cells is between ε1 and ε2,i.e.,ε1<εeq<ε2BThe quivalent emf εeq is smaller than ε1CThe εeq is given by εeq=ε1+ε2 alwaysDεeq is independent of internal resistances r1 and r2
AThe equivalent emf εeq of the two cells is between ε1 and ε2,i.e.,ε1<εeq<ε2BThe quivalent emf εeq is smaller than ε1CThe εeq is given by εeq=ε1+ε2 alwaysDεeq is independent of internal resistances r1 and r2
Find the emf (V) and internal resistance (R) of a single battery which is equivalent toa parallel combination of two batteries of emf V1 and V2 and internal resistances r1 and r2 respectively, with polrities as shown in figure
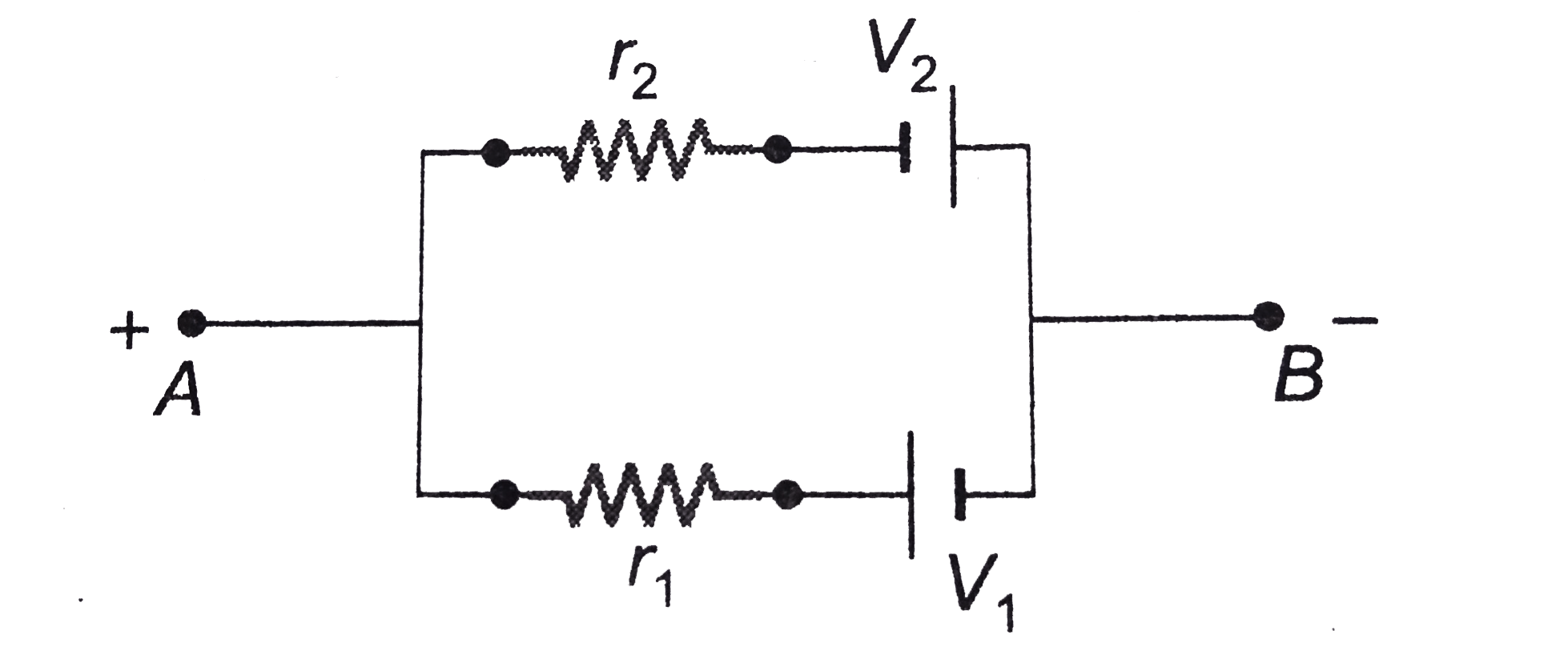
View Solution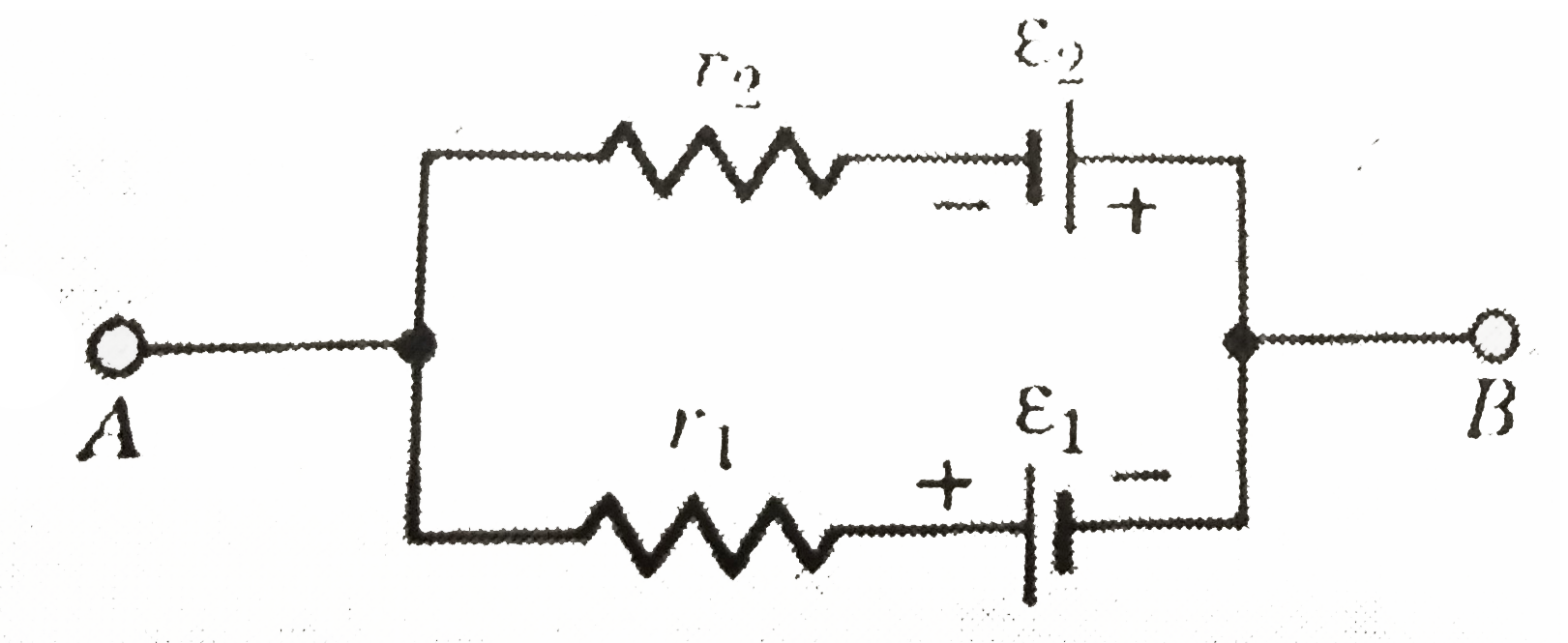
find the emf (ε0) and internal resistance (r0) if a battery which is equivalent to a parallel combination of two batteries of emfs ε1andε2 and internal resistances r1andr2 respectively, with polarities as shown in figure.
View SolutionTwo batteries of e.m.f. E1 and E2 and internal resistance r1 and r2 are connected in parallel. Determine their equivelent e.m.f.
View SolutionFind the emf (V) and internal resistance (r) of a single battery which is equivalent to a parallel combination of two batteries of emf's V1,andV_(2), and internal resistance r1 and r2 respectively, with polarities as shown in the figure
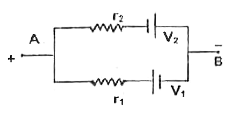
View SolutionTwo batteries of emf e1ande2 having internal resistance r1andr2 respectively are connected in series to an external resistance R. Both the batteries are getting discharged. The above described combination of these two batteries has to produce a weaker current than when any one of the batteries is connected to the same resistor. For this requirement to be fulfilled
View Solution
