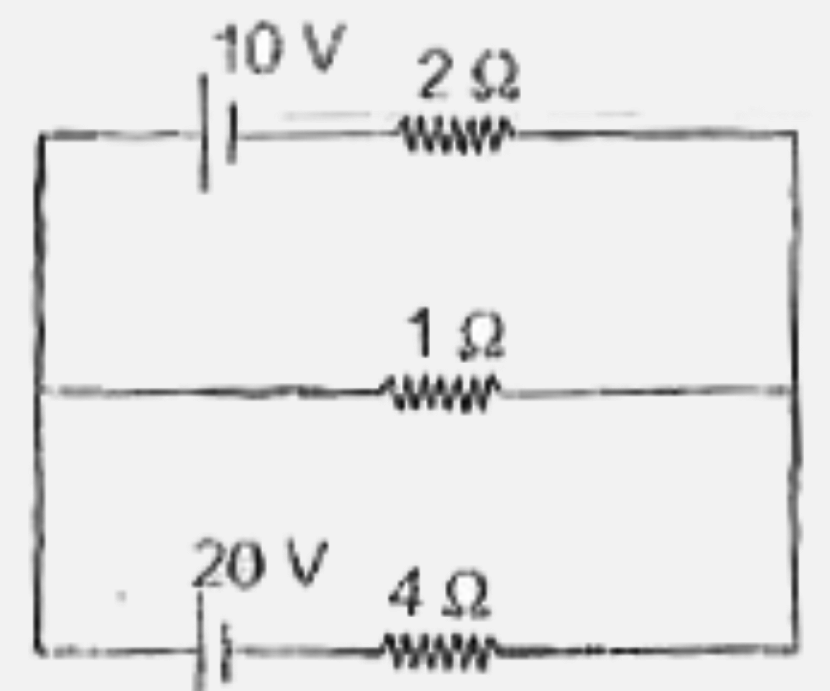
The resistances in the four arms of a Wheatstone network in cyclic order are 5Ω,2Ω,6Ω and 15Ω . If a current of 2.8 A enters the junction of 5Ω and 15Ω, then the current through 2Ω resistor is-
1.5 A
2.8 A
0.7 A
2.1 A
The correct Answer is:D
To solve the problem, we need to analyze the Wheatstone bridge circuit and apply the current divider rule. Here’s a step-by-step breakdown of the solution:
Step 1: Identify the resistances in the Wheatstone bridge
The resistances in the four arms of the Wheatstone network are:
- R1 = 5 Ω
- R2 = 2 Ω
- R3 = 6 Ω
- R4 = 15 Ω
Step 2: Calculate the equivalent resistances
The resistors R1 (5 Ω) and R2 (2 Ω) are in series, so their equivalent resistance (R_eq1) is:
Req1=R1+R2=5Ω+2Ω=7Ω
The resistors R3 (6 Ω) and R4 (15 Ω) are also in series, so their equivalent resistance (R_eq2) is:
Req2=R3+R4=6Ω+15Ω=21Ω
Step 3: Determine how the equivalent resistances are connected
The two equivalent resistances R_eq1 (7 Ω) and R_eq2 (21 Ω) are connected in parallel.
Step 4: Apply the current divider rule
We know that a current of 2.8 A enters the junction of the 5 Ω and 15 Ω resistors. We need to find the current through the 2 Ω resistor (which is in series with the 5 Ω resistor).
Using the current divider rule, the current through the 2 Ω resistor (I_2) can be calculated as follows:
I2=I×Req2Req1+Req2
Where:
- I = 2.8 A (total current entering the junction)
- R_eq1 = 7 Ω
- R_eq2 = 21 Ω
Step 5: Substitute the values
Substituting the values into the equation:
I2=2.8A×21Ω7Ω+21Ω
I2=2.8A×21Ω28Ω
Step 6: Simplify the equation
I2=2.8A×2128
I2=2.8A×34
I2=2.8A×0.75
I2=2.1A
Final Answer
The current through the 2 Ω resistor is 2.1 A.
---
The resistances in the four arms of the Wheatstone network are:
- R1 = 5 Ω
- R2 = 2 Ω
- R3 = 6 Ω
- R4 = 15 Ω
The resistors R1 (5 Ω) and R2 (2 Ω) are in series, so their equivalent resistance (R_eq1) is:
Req1=R1+R2=5Ω+2Ω=7Ω
Req2=R3+R4=6Ω+15Ω=21Ω
The two equivalent resistances R_eq1 (7 Ω) and R_eq2 (21 Ω) are connected in parallel.
We know that a current of 2.8 A enters the junction of the 5 Ω and 15 Ω resistors. We need to find the current through the 2 Ω resistor (which is in series with the 5 Ω resistor).
I2=I×Req2Req1+Req2
Where:
- I = 2.8 A (total current entering the junction)
- R_eq1 = 7 Ω
- R_eq2 = 21 Ω
Substituting the values into the equation:
I2=2.8A×21Ω7Ω+21Ω
I2=2.8A×21Ω28Ω
I2=2.8A×2128
I2=2.8A×34
I2=2.8A×0.75
I2=2.1A
The current through the 2 Ω resistor is 2.1 A.
Topper's Solved these Questions
- BOOK - ERRORLESSCHAPTER - CURRENT ELECTRICITYEXERCISE - NCERT BASED QUESTIONS (HEATING EFFECT OF CURRENT)67videos
CURRENT ELECTRICITY
- BOOK - ERRORLESSCHAPTER - CURRENT ELECTRICITYEXERCISE - PAST YEARS QUESTIONS76videos
CURRENT ELECTRICITY
- BOOK - ERRORLESSCHAPTER - CURRENT ELECTRICITYEXERCISE - NCERT BASED QUESTIONS (KIRCHHOFF.S LAW, CELLS)53videos
CURRENT ELECTRICITY
- BOOK - ERRORLESSCHAPTER - ATOMIC AND NUCLEAR PHYSICSEXERCISE - Assertion and Reason23videos
ATOMIC AND NUCLEAR PHYSICS
- BOOK - ERRORLESSCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - ASSERTION & REASON20videos
ELECTROMAGNETIC INDUCTION
Similar Questions
Knowledge Check
- Question 1 - Select One
The resistance in the four arms of a Wheatstone network in cyclic order are 5Ω,2Ω,6Ωand15Ω. If a current of 2.8 A enters the junction of 5Ω and 15Ω, then the current through 2Ω resistor is
A1.5 AB2.8 AC0.7 AD2.1 A - Question 2 - Select One
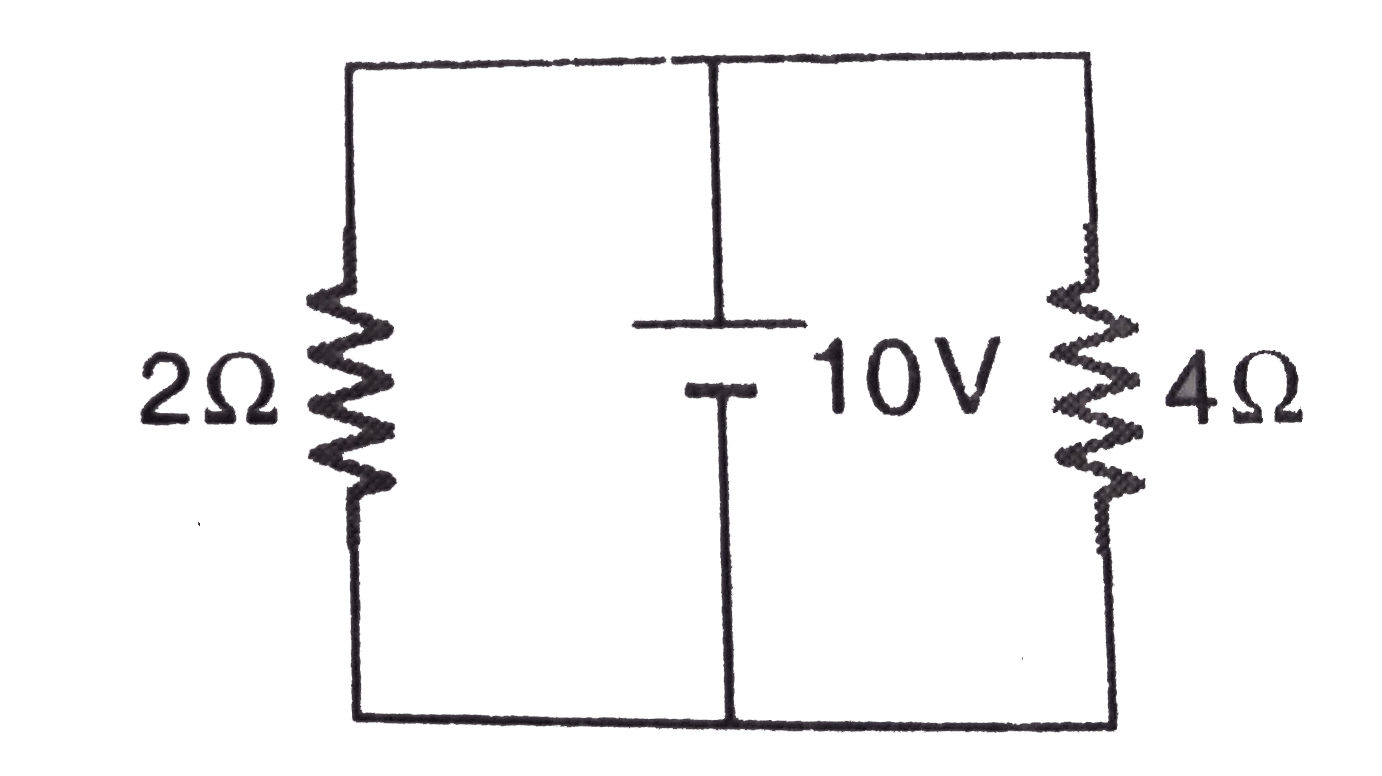
Current through the 5Ω resistor is
 A2AB4ACzeroD1A
A2AB4ACzeroD1A - Question 3 - Select One
In the figure shown the current through 2Ω resistor is
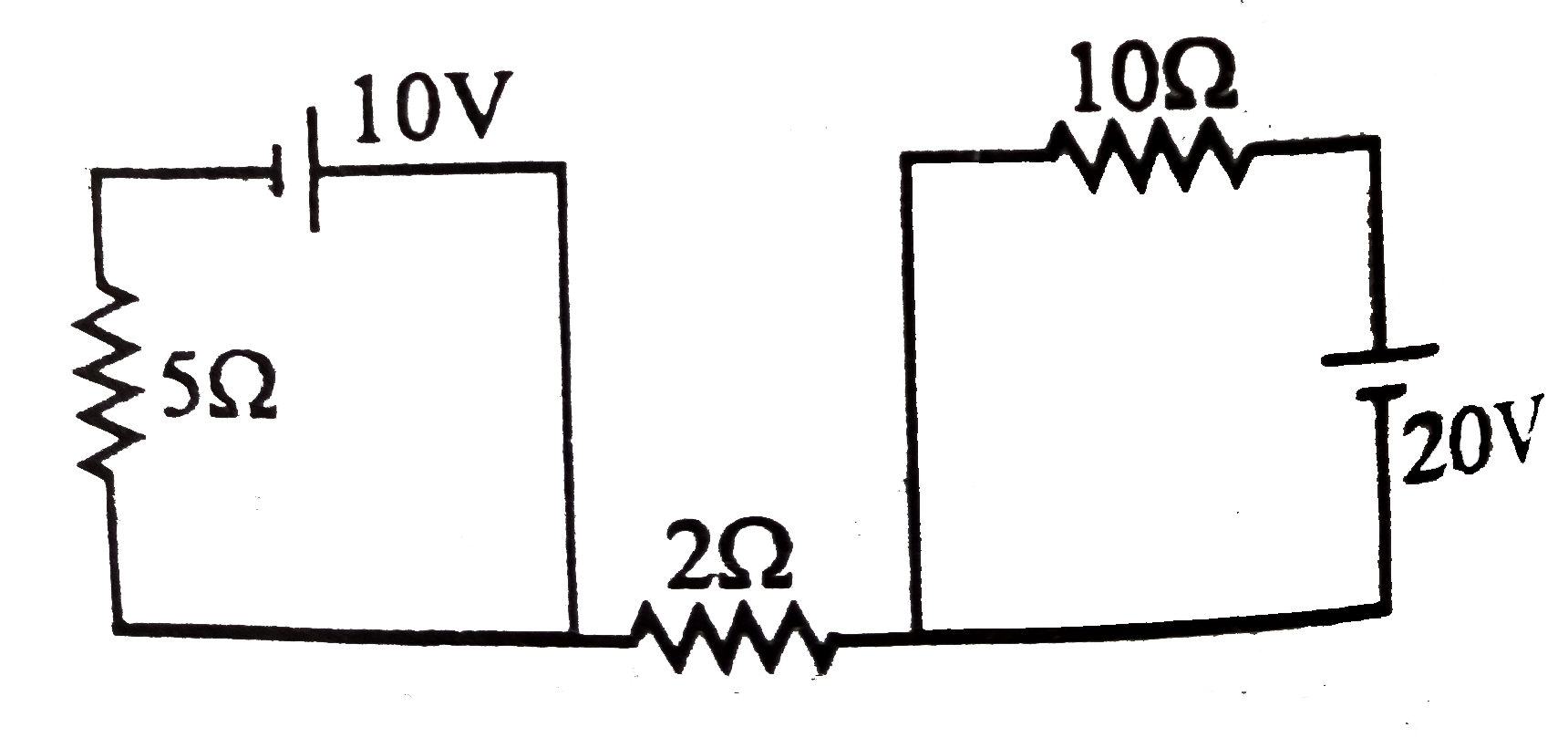 A2AB0AC4AD6A
A2AB0AC4AD6A
Four resistances arranged to form a Wheatstone network are 8Ω,12Ω,6Ω and 27Ω resistance, so that the bridge is balanced, is
View SolutionFind the current in 2Ω resistance.
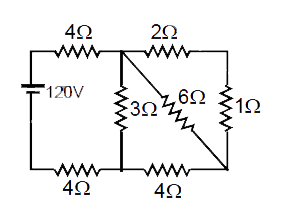 View Solution
View SolutionIn the arrangement the current through 5Ω resistor is
 View Solution
View SolutionFor resistances arranged to form a wheatstone's network are 10Ω,15Ω,6Ωand36Ω. What resistance should be connected across the 36Ω resistance to balance the bridge ?
View SolutionIn a typical Wheatstone network, the resistances in cyclic order are A=10Ω,B=5Ω,C=4Ω D=4Ω for the bridge to be balanced
 View Solution
View Solution