Three identical particles are joined together by a thread as shown in figure. All the three particles are moving in a horizontal plane. If the velocity of the outermost particle is v0, then the ratio of tensions in the three sections of the string is (TBC:TAB:TDA)

3:5:7
3:4:5
7:11:6
3:5:6
The correct Answer is:D
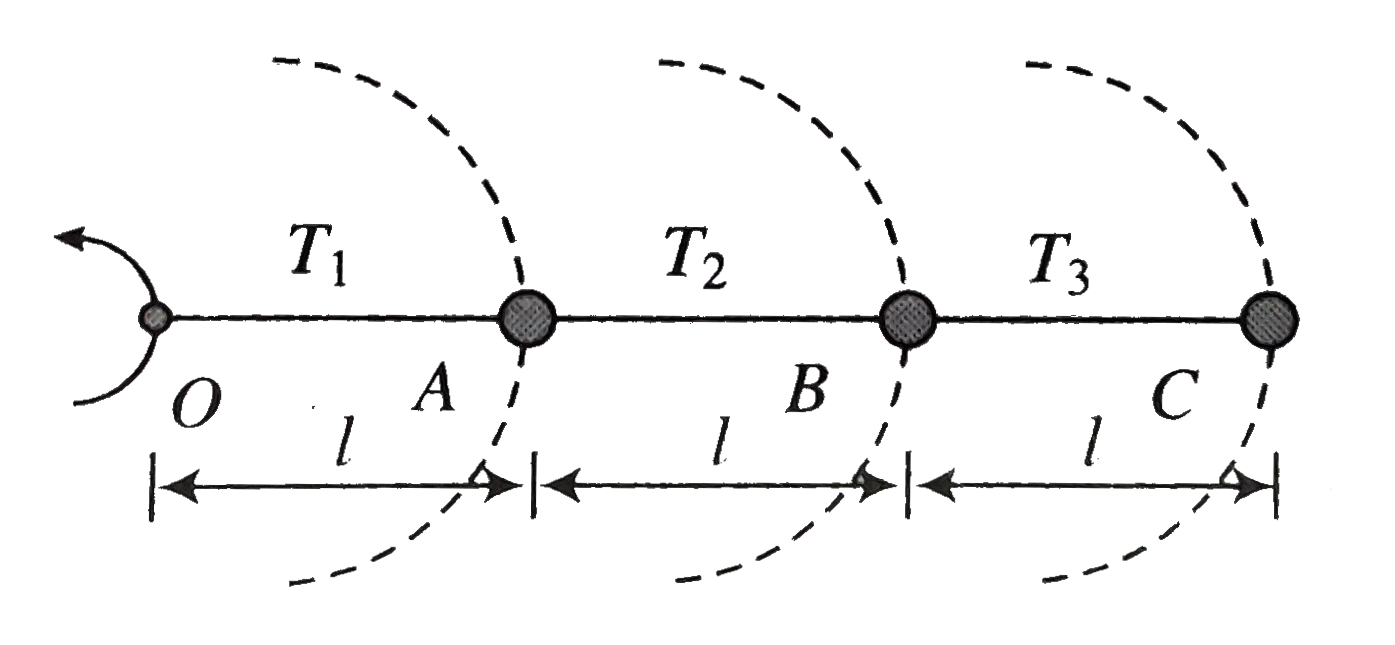
T3=mω2(3l)
T2−T3=mω2(3r)
T1−T2=mω2(r)
⇒T1=mω2(4r)
T1:T2=4:3

Similar Questions
T_(1) , T_(2) and T_(3) are tensions in the three strings. Then T_(1) : T_(2) is (##CHY_DMB_PHY_XI_P2_QP_19_E01_005_Q01.png" width="80%">
View Solutionतीन एक समान कण किसी डोरी द्वारा चित्रानुसार आपस में जुड़े हैं। सभी तीनों कण क्षैतिज तल में गति कर रहे हैं यदि बाह्यतम कण का वेग v0, हो तो डोरी के तीनों भागों में तनावों का अनुपात है
View Solutionतीन समान कण एक साथ चित्रानुसार एक धागे से बँधे हैं | तीनो कण क्षैतिज समतल में घूम रहे हैं | यदि सबसे बाहर वाले कण का वेग v0 है, तब रस्सी (धागे) के तीनो भागो के तनावों का अनुपात है

View SolutionThree identical particles are connected together as pictured by a doro. All three particles are moving in the bottom plane. If the velocity ratio of the outermost particle is, then the ratio of stresses in all three parts of the string.
View SolutionThree blocks connected together by strings are pulled along a horizontal surface by applying force F. If T_(3)=36 N , What is tension T_(2) ?
View SolutionThree identical particles are joined together by a thread as shown in figure. All the three particles are moving in a horizontal plane. If the velocity of the outermost particle is v_(0) , then the ratio of tensions in the three sections of the string is (T_(BC):T_(AB):T_(DA))
View SolutionThree identical particles are joined together by a thread as shown in figure All the partical are moving in a horizontal plane If the vertical of the outermost particle is v0 then the ratio of tension in the three sections of the string (T1:T2:T3=?) is
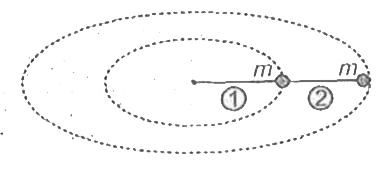
View SolutionTwo particles each of mass m are moving in horizontal circle with same angular speed. If both string are of same length then the ratio of tension in string T1T2 is
View Solution
