A ball is thrown from the ground into air. AT a height of 9.0m, the velocity is observed to be →v=7.0ˆi+6.0ˆj. Find the maximum height to which the ball will rise. g=10,s−2.
The correct Answer is:11
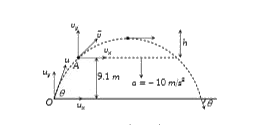
Velocity at a=(76ˆi+6.1ˆj)
∴ Initial vertical velocity at A=(6.1)ˆjm/s Find vertical velocity at B = 0
Using v2=u2=2as (between A and B)
⇒0=(6.1)2+2(−10)(+h)
⇒h=1.86m
∴ maximum height attained by ball
=9.1+1.86=10.96m≈11m
Similar Questions
H ऊँचाई से एक गेंद को फेंका जाता है और इसके प्रक्षेपण से 1.5s बाद गेंद फर्श से 10(ˆi−ˆj) वेग के साथ टकराती है। गेंद की प्रारम्भिक चाल ज्ञात कीजिए।
View SolutionA projectile is given an initial velocity of (ˆi+2ˆj)m/s, where ˆi is along the ground and ˆj is along the vertical . If g=10m/s2, the equation of its trajectory is :
View SolutionA body is projected from the ground with a velocity vec(v)= (3 hat(i) + 10 hat(j)) ms^(-1) . The maximum height attained and the range of the body respectively are (given g= 10 ms^(-2) )
View SolutionA projectile is projected in air with initial velocity →v=(3ˆi+4ˆj) m/s from the origin. The equation of trajectory of the projectile is given as (g=−10ˆjms2) (neglect air resistance )
View SolutionA projectile is thrown with an initial velocity of v=aˆi+bˆj. If the range of projectile is double the maximum height reached by it. Find the ratio ba.
View SolutionAt a height 0.4 m from the ground the velocity of a projectile in vector form is vec v = (6 hat i+ 2 hat j) ms ^-1 . The angle of projection is
View SolutionA projectile is given an initial velocity of (ˆi+2ˆj)m/s, where ˆi is along the ground and ˆj is along the vertical . If g=10m/s2, the equation of its trajectory is :
View SolutionA projectile is projected in air with initial velocity vec v=(3 hat i + 4 hat j) m/s from the origin. The equation of trajectory of the projectile is given as (g=-10 hat j m/s^2) (neglect air resistance )
View Solution
