Three wires of length l1,l2,l3 form a triangle surrounted by another circular wire, if l3 is the diameter and l3=2l1, then the angle between la and l3 will be
30∘
60∘
45∘
90∘
The correct Answer is:B
Topper's Solved these Questions
- CIRCLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - CIRCLESEXERCISE - Exercise (LEVEL -2)
20 Videos
- CIRCLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - CIRCLESEXERCISE - Exercise (Match the following)
6 Videos
- CIRCLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - CIRCLESEXERCISE - NCERT Section (Exercise 10.2)
16 Videos
- ARITHMETIC PROGRESSIONS BOOK - MTG IIT JEE FOUNDATIONCHAPTER - ARITHMETIC PROGRESSIONS EXERCISE - OLYMPIAD/HOTS CORNER
15 Videos
- CO-ORDINATE GEOMETRYBOOK - MTG IIT JEE FOUNDATIONCHAPTER - CO-ORDINATE GEOMETRYEXERCISE - Olympiad/HOTS Corner
40 Videos
Similar Questions
Three wires of lengths L1,L2,L3 and Youngs moduli Y1,Y2andY3 respectively are pulled by a force F as shown in fig. The extensions produced in wires are ΔL1,ΔL2,ΔL3
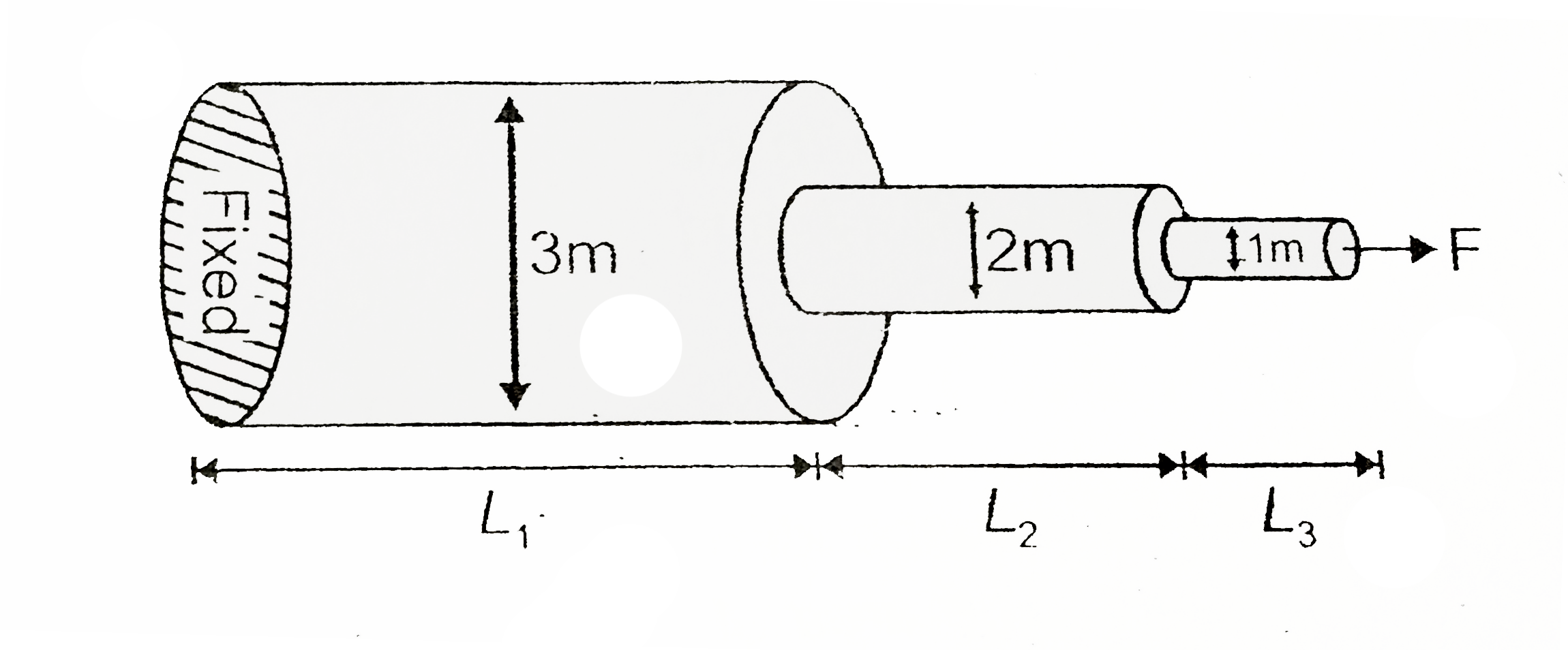
Match the Column-I with Column-II
Column-I Column-II(A) If 9L2=4L1andΔL1=ΔL2, then(p) Y2=Y1(B) If L2<4L3andΔL2=ΔL2, then(q) Y2>Y1(C) If ΔL1=ΔL2andL1=L2, then(r) Y2<Y3(D) If L2=L3andΔL2=ΔL3, then(s) 4Y2=Y3
View SolutionThree wires of lengths L1,L2,L3 and Youngs moduli Y1,Y2andY3 respectively are pulled by a force F as shown in fig. The extensions produced in wires are ΔL1,ΔL2,ΔL3

Match the Column-I with Column-II
Column-I Column-II(A) If 9L2=4L1andΔL1=ΔL2, then(p) Y2=Y1(B) If L2<4L3andΔL2=ΔL2, then(q) Y2>Y1(C) If ΔL1=ΔL2andL1=L2, then(r) Y2<Y3(D) If L2=L3andΔL2=ΔL3, then(s) 4Y2=Y3
View Solution
Knowledge Check
The resistance of a wire of uniform diameter d and length L is R . The resistance of another wire of the same material but diameter 2d and length 4L will be
A2RBRCR/2DR/4Two wire have length 'l1'and'l2' carries equal current Two circular loop made by these wires, then ratio of their magnetic moment is 3 : 2 respectively then length ratio of wires respectively:
A9:4B4:9C√3:√2D√2:√3When a string is divided into three segments of lengths l1,l2andl3 the fundamental frequencies of these three segments are v1,v2andv3 respectively. The original fundamental frequency (v) of the string is
A√v=√v1+√v2+√v3Bv=v1+v2+v3C1v=1v1+1v2+1v3D1√v=1√v1+1√v2+1√v3
Consider the lines given by : L1:x+3y−5=0,L2:3x−ky−1=0,L3:5x+2y−12=0 If a be the value of k for which lines L1,L2,L3 do not form a triangle and c be the value of k for which one of L1,L2,L3 is parallel to at least one of the other lines, then abc=
View SolutionConsider the lines given by : L1:x+3y−5=0,L2:3x−ky−1=0,L3:5x+2y−12=0 If a be the value of k for which lines L1,L2,L3 do not form a triangle and c be the value of k for which one of L1,L2,L3 is parallel to at least one of the other lines, then abc=
View SolutionIf l1,l2,l3 are respectively the perpendicular from the vertices of a triangle on the opposite side, then show that l1l2l3=a2b2c28R3.
View SolutionThree straight lines l1,l2 and l3 are parallel and lie in the same plane. Five points are taken on each of l1,l2 and l3. The maximum number of triangles which can be obtained with vertices at these points, is
View SolutionWhen a string is divided into three segments of length l1,l2 and l3 the fundamental frequencies of these three segments are f1,f2 and f3 respectively. The original fundamental frequency f of the string is
View Solution
