ABCD is a parallelogram. The circle through A, B and C intersects CD produced at E. Which of the following is true ?
∠ABC=∠AEC
∠ADE=∠AED
AE=BC
Both b and c
The correct Answer is:D
Topper's Solved these Questions
- CIRCLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - CIRCLESEXERCISE - Exercise (LEVEL -2)
20 Videos
- CIRCLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - CIRCLESEXERCISE - Exercise (Match the following)
6 Videos
- CIRCLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - CIRCLESEXERCISE - NCERT Section (Exercise 10.2)
16 Videos
- ARITHMETIC PROGRESSIONS BOOK - MTG IIT JEE FOUNDATIONCHAPTER - ARITHMETIC PROGRESSIONS EXERCISE - OLYMPIAD/HOTS CORNER
15 Videos
- CO-ORDINATE GEOMETRYBOOK - MTG IIT JEE FOUNDATIONCHAPTER - CO-ORDINATE GEOMETRYEXERCISE - Olympiad/HOTS Corner
40 Videos
Similar Questions
Knowledge Check
In the figure, ABCD is a parallelogram. Which one of the following is true?
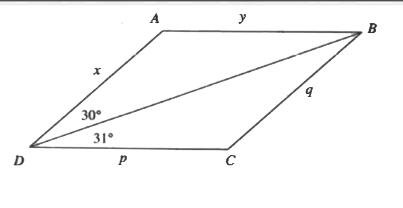 Ax<yBx>qCx>pDy>p
Ax<yBx>qCx>pDy>p
ABCD is a parallelogram. The circle through A,BandC intersects CD produced at E, prove that AE=AD.
View SolutionABCD is a parallelogram. The circle through A,BandC intersects CD produced at E, prove that AE=AD.
View SolutionABCD is a parallelogram. The circle through A, B and C intersect CD (produced ifnecessary) at E. Prove that AE = AD.
View SolutionABCD is a parallelogram . The circle passing through the vertices. A, B and C intersects CD (or CD produced) at E. Prove that AE=AD.
View SolutionABCD is a parallelogram . The circle passing through the vertices. A, B and C intersects CD (or CD produced) at E. Prove that AE=AD.
View SolutionABCD is a parallelogram. A circle through A, B is so drawn that it intersects AD at P and BC at Q. Prove that P, Q, C and D are concyclic.
View SolutionABCD is a parallelogram. A circle through A, B is so drawn that it intersects AD at P and BC at Q. Prove that P, Q, C and D are concyclic.
View Solution
