In the given figure, O is the centre and AOC is a diameter of the circle. Find
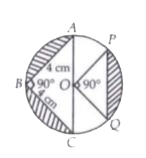
The ares of the designed segment made by the chord PQ.
The correct Answer is:
Topper's Solved these Questions
- AREAS RELATED TO CIRCLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - AREAS RELATED TO CIRCLESEXERCISE - EXERCISE (INTEGER/NUMERICAL VALUE TYPE)
20 Videos
- AREAS RELATED TO CIRCLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - AREAS RELATED TO CIRCLESEXERCISE - OLYMPIAD/HOTS CORNER
30 Videos
- AREAS RELATED TO CIRCLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - AREAS RELATED TO CIRCLESEXERCISE - EXERCISE (SUBJECTIVE PROBLEMS ( VERY SHORT ANSWER))
16 Videos
- ARITHMETIC PROGRESSIONS BOOK - MTG IIT JEE FOUNDATIONCHAPTER - ARITHMETIC PROGRESSIONS EXERCISE - OLYMPIAD/HOTS CORNER
15 Videos
Similar Questions
Knowledge Check
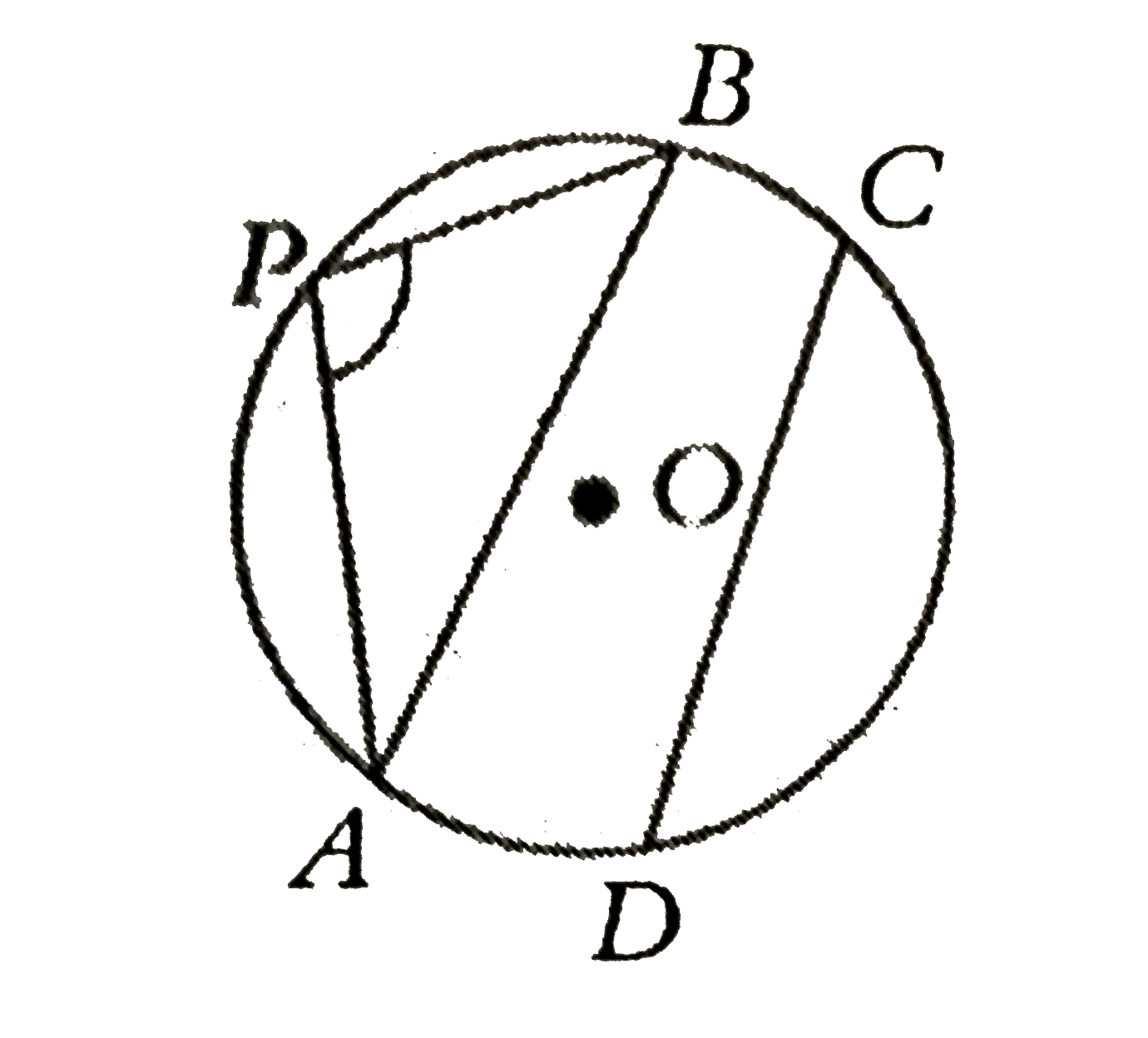
In the above figure, O is the centre of the circle and AB=CD. If ∠APB=110∘, then find the angle made by the chord CD at the centre.A220∘B110∘C120∘D140∘
In given figure, O is the centre of the circle.
A chord, which is not the diameter of the circle is
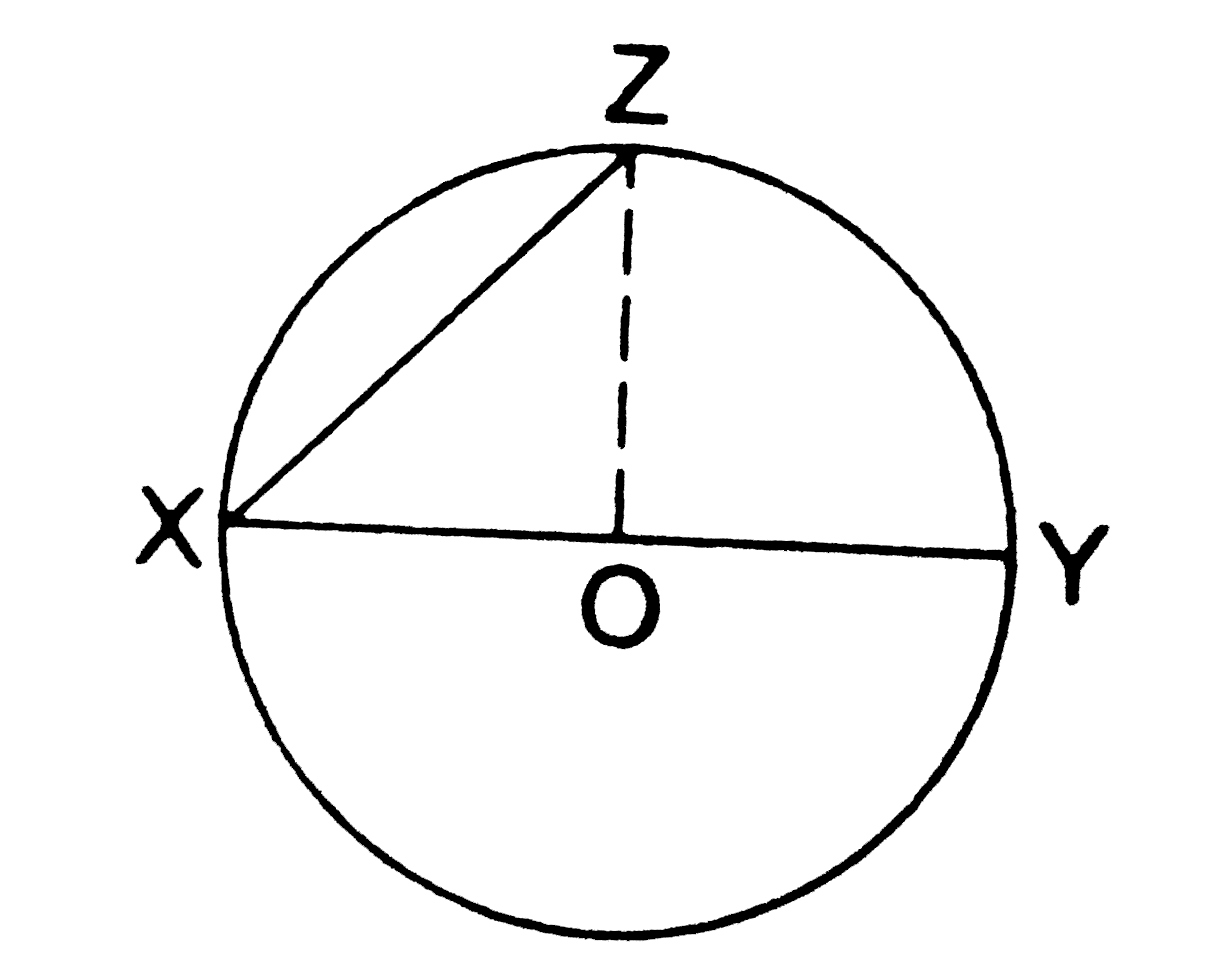
View SolutionIn the given figure, O is the centre of the circle and XOY is a diameter. If XZ is any other chord, show that XY gt XZ.
View Solution
In the above figure, O is the centre of the circle and AB=CD. If ∠APB=110∘, then find the angle made by the chord CD at the centre.
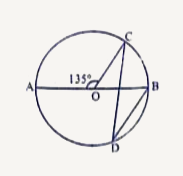
View SolutionIn the figure, AB is the diameter of the circle. If ∠AOC=135∘ then find the ∠CDB.
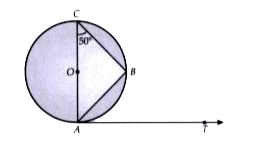
View SolutionIn the given figure A,B is a chord of the circle and AOC is its diameter ,such that ∠ACB=50∘ .If AT is the tangent to the circle at the point A, then ∠BAT is equal to :
View SolutionIn the figure, O is the centre of the circle. Prove ∠AOC=∠AFC+∠AEC.
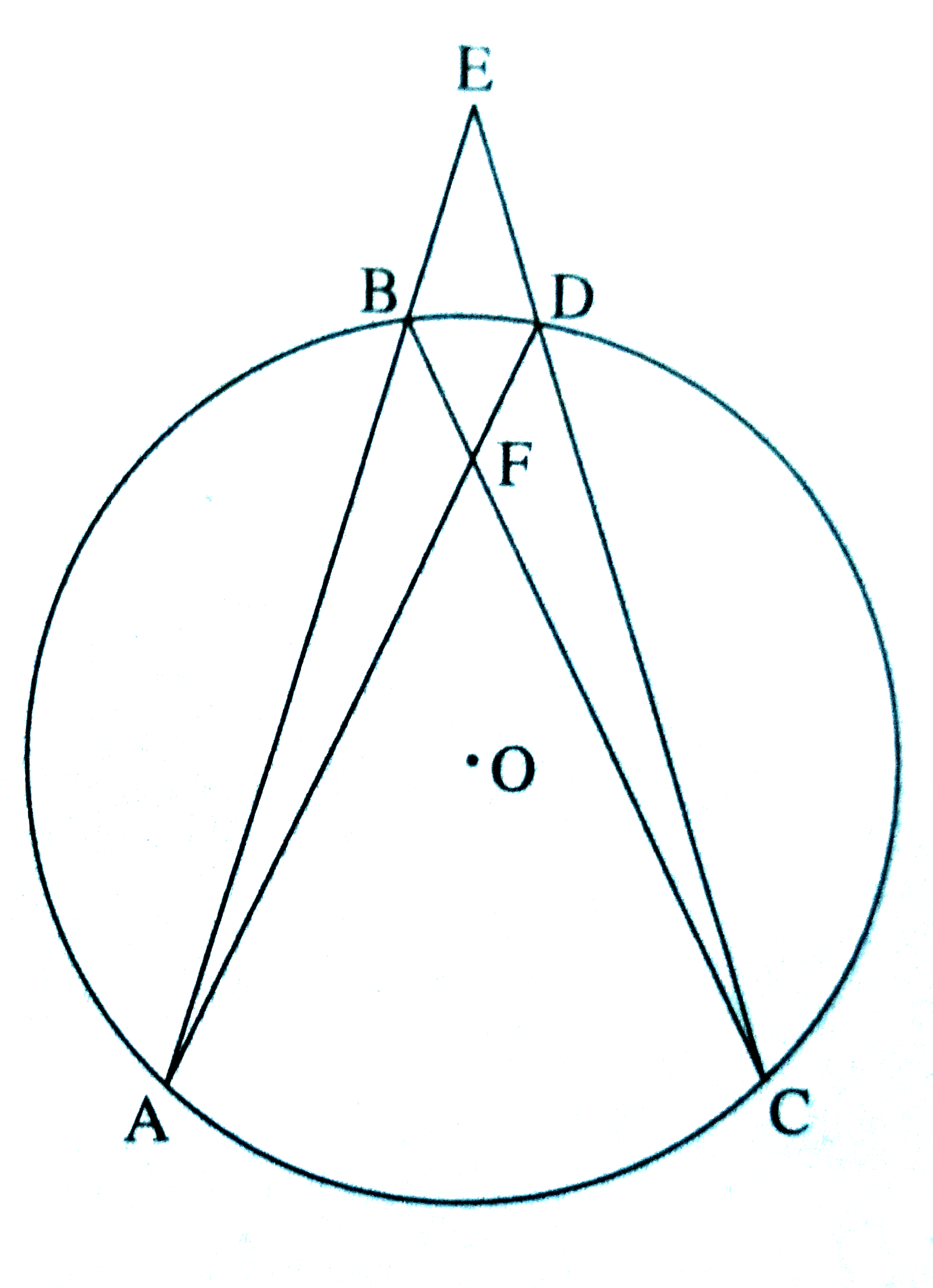
View SolutionIn the given figure, if O is the centre of the circle , PQ is a chord.
∠POQ=90∘ area of shaded region is 144cm2, Find the radius of the circle . (pi =3.14)

∠POQ=θ=90∘
A(shaded ergion)=A(segment PRQ) =114cm2,π=3.14
To find: radius of the circle (r)
View Solution


