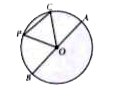
In the given figure, O is the centre and AOC is a diameter of the circle. Find
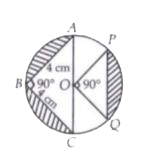
The sum of the areas of the two designed segment made by chords AB and BC.
The correct Answer is:4.56cm2
Topper's Solved these Questions
- AREAS RELATED TO CIRCLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - AREAS RELATED TO CIRCLESEXERCISE - EXERCISE (INTEGER/NUMERICAL VALUE TYPE)
20 Videos
- AREAS RELATED TO CIRCLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - AREAS RELATED TO CIRCLESEXERCISE - OLYMPIAD/HOTS CORNER
30 Videos
- AREAS RELATED TO CIRCLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - AREAS RELATED TO CIRCLESEXERCISE - EXERCISE (SUBJECTIVE PROBLEMS ( VERY SHORT ANSWER))
16 Videos
- ARITHMETIC PROGRESSIONS BOOK - MTG IIT JEE FOUNDATIONCHAPTER - ARITHMETIC PROGRESSIONS EXERCISE - OLYMPIAD/HOTS CORNER
15 Videos
Similar Questions
Knowledge Check
In a circle with the centre is O and AB is the diameter of the circle and CD is the chord of the circle. If angle ABC is 54∘ and the length of CD and BC is equal, then find the ∠DBC.
A1. 36∘B2. 24∘C3. 48∘D4. 12∘
In the figure, AB is a diameter of the circle with centre O and OA = 7cm. Find the area of the shaded region
View SolutionIn the figure, AB is a diameter of the circle with centre O and OA = 7cm. Find the area of the shaded region
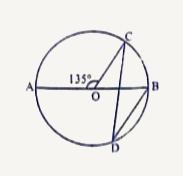
View SolutionIn the figure, AB is the diameter of the circle. If ∠AOC=135∘ then find the ∠CDB.
View SolutionIn the adjoining figure, O is the centre of the circle and AB is its diameter. If AC=8 cm and BC= 6cm, then find the radius of the circle.

View SolutionIn the adjoining figure, O is the centre of the circle and AB is its diameter. If AC=8 cm and BC= 6cm, then find the radius of the circle.

View SolutionIn the given figure, O is the centre of the bigger circle and AC is its diameter. Another circle with AB as diameter is drawn. If AC = 54 cm and BC = 10 cm. Find the area of the shaded region

View SolutionIn the given figure, O is the centre of the bigger circle and AC is its diameter. Another circle with AB as diameter is drawn. If AC = 54 cm and BC = 10 cm. Find the area of the shaded region

View Solution