In ‘Less Than' Ogive, the cumulative frequencies are written corresponding to the (P) limits of the classes of the given data.
In 'More Than' Ogive, the cumulative frequencies are written corresponding to the (Q) limits of the classes.
On an ogive, point P whose y-coordinate =π/2 (i.e, half of the total number of the entries), has its x-coordinate equal to the (R) of the data
Two ogives, one less than type and the other more than type for the same data when drawn simultaneously on the same graph intersect each other at the point P whose (S) =n/2 and (T) = median of the data where it is the total number of the entries of the data.
P-upper, Q-Lower, R-Median, S-y-coordinate, T-x-coordinate
P-Lower, Q-upper, R-Median, S-y-coordinate, T-x-coordinate
P-upper, Q-Lower, R-Median, S-x-coordinate, T-y-coordinate
P-upper, Q-Lower, R-Upper limit, S-y-coordinate, T-x-coordinate
The correct Answer is:A
Topper's Solved these Questions
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - STATISTICSEXERCISE - Exercise (Subjective (Integer/Numerical Value Type))18videos
STATISTICS
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - SOME APPLICATIONS OF TRIGONOMETRY EXERCISE - OLYMPIAD /HOTS CORNER20videos
SOME APPLICATIONS OF TRIGONOMETRY
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - OLYMPIAD/HOTS CORNER20videos
SURFACE AREAS AND VOLUMES
Similar Questions
Knowledge Check
- Question 1 - Select One
The abscissa of the point of intersection of less than type and more than type ogives gives its
AmeanBmodeCmedianDall the three measures - Question 2 - Select One
In 'Less than' cumulative frequency distribution the omitted limit is
ALowerBUpperCMiddleDNone of these - Question 3 - Select One
The cumulative frequency proceeding to the median class for the following data is
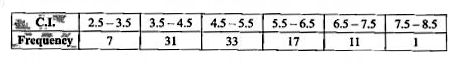 A71B88C38D40
A71B88C38D40
Construct a less than ogive and a more than ogive from the following data :
 View Solution
View SolutionDraw 'less than' as well as 'more than' ogives for the following data :
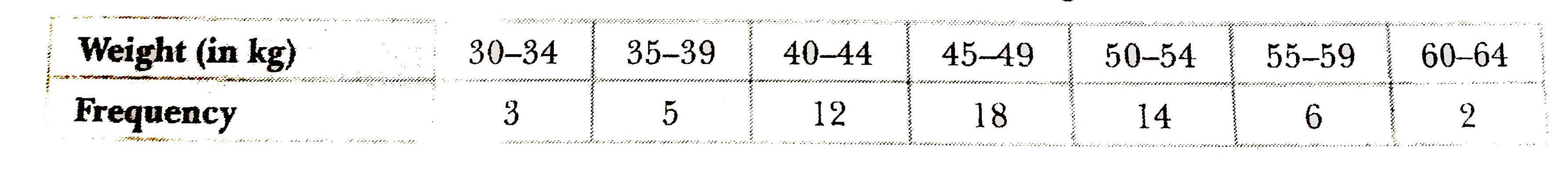 View Solution
View SolutionDraw a 'less than' ogive for the following frequency distribution:
View SolutionThe 'less than' ogive curve and the 'more than' ogive curve intersect at
View SolutionIf the 'less than ' and the 'more than' ogive given intersect at the point (27,34) , then find the median of the distribution and also find the total number of observations .
View Solution


