A stone is allowed to fall from the top of a tower 100 m high and at the same time another stone is projected vertically upwards from the ground with a velocity of 25 m/s. Calculate when and where the two stones will meet.
Here, h = 100 m.
Let the two stones meet after t seconds at a point P which is at a height x above the ground as shown in figure.
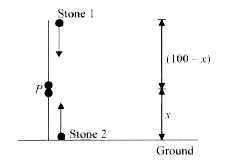
For stone 1,
u = 0, h = (100 - x) m,
a=g=9.8m/s2
From s = ut + 12 gt2
(100−x)=0+12×9.8t2=4.9t2 ...(i)
For stone 2,
u=25m/s,h=x,a=g=−9.8m/s2
From s = ut +12at2
x=25t+12(−9.8)t2=25t−4.9t2 ....(ii)
Adding equations (i) and (ii)
100−x+x=25t⇒t=10025=4s
From equation (i),
100−x=4.9×(4)2=78.4
x = 100 - 78.4 = 21.6 m
Topper's Solved these Questions
- GRAVITATION Book:MTG IIT JEE FOUNDATIONChapter:GRAVITATION Exercise:Exercise (Multiple Choice Questions) (LEVEL - 1)
Explore 30 Videos
- GRAVITATION Book:MTG IIT JEE FOUNDATIONChapter:GRAVITATION Exercise:Exercise (Multiple Choice Questions) (LEVEL - 2)
Explore 20 Videos
- GRAVITATION Book:MTG IIT JEE FOUNDATIONChapter:GRAVITATION Exercise:Solved Examples
Explore 10 Videos
- FORCE AND LAWS OF MOTIONBook:MTG IIT JEE FOUNDATIONChapter:FORCE AND LAWS OF MOTIONExercise:OLYMPIAD /HOTS CORNER
Explore 20 Videos
- MOTIONBook:MTG IIT JEE FOUNDATIONChapter:MOTIONExercise:Olympiad/HOTS Corner
Explore 21 Videos
Similar Questions
A stone is allowed to fall from the top of a tower 100m high and at the same time another stone is projected vertically upwards from the ground with a velocity of 25ms.Calculate when and where the two stones will meet.
View SolutionA stone is allowed to fall from the top of a tower 100m high and at the same time another stone is projected vertically upwards from the ground with a velocity of 25m/s. Calculate when and where the two stone will meet.
View Solution
Knowledge Check
A stone is dropped from the top of a 400m high tower. At the same time another stone is projected vertically upwards from the ground with a speed of 50m/s. The two stones will cross each other after a time
A2 sB4 sC6 sD8 s
A stone is allowed to fall from the top of a tower 100m high and at the same time another stone is projected vertically upwards from the ground with a velocity of 25m/s. Calculate when and where the two stones will meet.
View Solution
A stone is allowed to fall from the top of a tower 300 m height and at the same time another stone is projected vertically up from the ground with a velocity 100m/s. Find when and where the two stones meet?
View SolutionA stone is allowed to fall from the top of a tower 300 m height and at the same time another stone is projected vertically up from the ground with a velocity 100ms−1 . Find when and where the two stones meet ?
View SolutionA stone is dropped from the top of a tower 200 m high. At the same time, another stone is projected vertically upwards from the ground with a velocity of 40m/s. Calcuate when and where the two stones will mest.
View SolutionForm the top of a tower 100m in height a ball is dropped and at the same time another ball is projected vertically upwards from the ground with a velcoity of 25ms−1. Find when and where the two balls will meet.
View SolutionA stone is dropped from a height 300 m and at the same time another stone is projected vertically upwards with a velocity of 100m/sec. Find when and where the two stones meet.
View SolutionFrom the top of a tower 100 m in height a ball is dropped and at the same time another ball is projected vertically upwards from the ground with a velocity of 25 m/s. Find when and where the two balls will meet? (g=9.8m/s)
View Solution
