A block of base 10cm×10cm and height 15cm is kept on an inclined plane. The corfficient of friction between them is √3. The inclination θ of this inclined plane from the horizontal plane is gradually increased frm 0∘. Then
At θ=30∘, the block will start sliding down the plane
The block will remain at rest on the plane up to certaiin θ and then it will topple
At θ=60∘, the block will start sliding down the plane and continue to do so at higher angles
At θ=60∘, the block will start sliding down the plane and on further increasing θ, it will topple at certain θ
The correct Answer is:B

For sliding :
tanθ≥√3≈1.732
For toppling ,
tanθ≥23≈0.67
Similar Questions
A block is released from the top of an inclined plane of inclination theta and height h. Time required to reach the foot of the inclined plane is
View SolutionAn uniform block of mass M, height h and base width a is kept on a rough inclined plane as shown in figure. Friction is enough to prevent any slipping between inclined plane and block. The angle of inclined plane is then increased. The limiting value of θ so that the block not tip over tan−1(xa/h) where 'x' is

View SolutionA block of mass m is placed at rest on an inclination θ to the horizontal. If the coefficient of friction between the block and the plane is μ, then the total force the inclined plane exerts on the block is
View SolutionA block with a square base measuring a×a and height h, is placed on an inclined plane. The coefficient of friction is μ. The angle of inclination (θ) of the plane is gradually increased. The block will
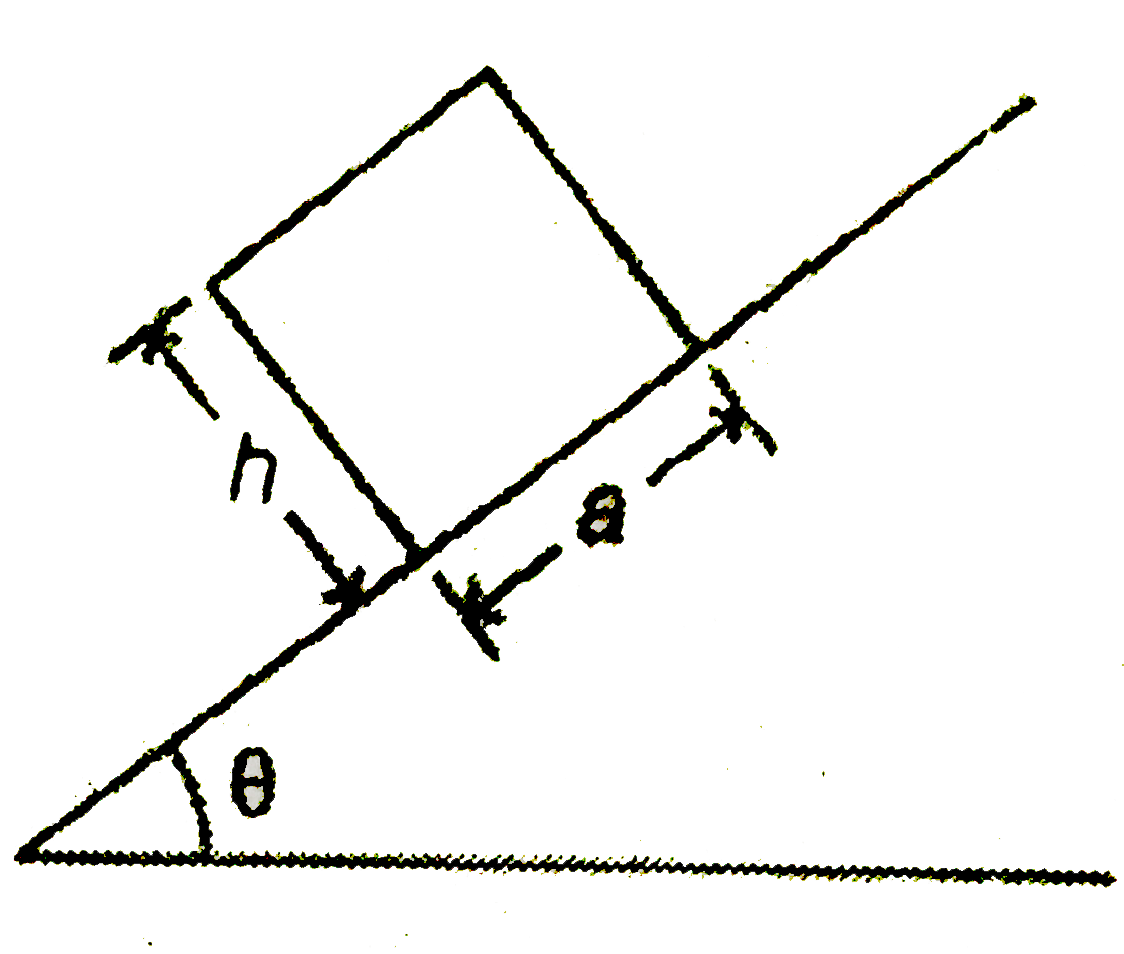
View SolutionA block of base 10cm×10cm and height 15cm is kept on an inclined plane. The coefficient of friction between them is √3. The inclination θ of this inclined plane from the horizontal plane is gradually increased from 0∘ Then
View SolutionAblock with a square base measuring axxa and height h, is placed on an inclined plane. The coefficient of friction is mu . The angle of inclination (theta) of the plane is gradually increased. The block will
View SolutionA block of mass m takes time t to slide down on a smooth inclined plane of angle of inclination theta and height h. If same block slids down on a rough inclined plane of same angle of inclination and same height and takes time n times of initial value, then coefficient friction between block and inclined plane is
View SolutionA block A is kept on a rough inclined plane. Initially θ=0. The co-efficient of kinetic friction between A and the inclined plane is √3 The angle θ is increased slowly. When θ becomes 60∘, then :

View Solution
