A particle of mass m is dropped from a height h above the ground. Simultaneously another particle of the same mass is thrown vertically upwards from the ground with a speed of√2gh. If they collide head-on completely inelastically, then the time taken for the combined mass to reach the ground is
3√38u2g
2√2u2g
58u2g
3√24u2g
The correct Answer is:A
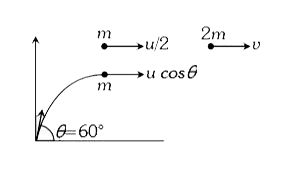
Pi=Pf [∵ by conservation of momentum]
mu+mucosθ=2mv
⇒v=u(1+cos60∘)2=34u
So horizontal range after collsion = vt
=v√2Hmaxg=34u√2u2sin2(60∘)2g2=34u2√34g=3√3u28g
Similar Questions
mass ‘m’ is projected vertically upwards with a speed ‘u’ and at the same instance another particle of mass ‘m’ is released from height ‘h’ vertically above the first particle. The two particles suffer a perfectly inelastic collision, and again reach a maximum height ‘h’ as one combined particle. What is the value of u?
View SolutionThere are two identical particles A and B. One is projected vertically upward with speed sqrt(2gh) from ground and other is dropped from height h along the same vertical line. Collision between them is perfectly inelastic. Find time taken by them to reach the ground after collision in terms of sqrt(h/g) .
View SolutionA body of mass .m. is dropped and another body of mass M is projected vertically up with speed .u. simultaneously from the top of a tower of height H. If the body reaches the heightst point before the dropped body reaches the ground, then maximum height raised by the centre of mass of the system from ground is
View SolutionA particle of mass m is dropped from a height h above the ground. At the same time another particle of mass 2m is thrown vertically upwards from the ground with a speed of sqrt(gh) . If they collide head-on completely inelastically, the time taken for the combined mass to reach the ground, in units of sqrt(h/g) is :
View SolutionA particle of mass 2 is dropped from a height 80 m above the ground. At the same time another particle of mass m is thrown vertically upwards from the ground with a speed of 40 m/s. If they collide head-on completely inelastically, the time taken for the combined mass to reach the ground, in units of second is:
View SolutionA body of mass m is dropped from a height of h . Simultaneously another body of mass 2m is thrown up vertically with such a velocity v that they collide at height h/2 . If the collision is perfectly inelastic, the velocity of combined mass at the time of collision with the ground will be
View SolutionA body of mass m is dropped from a height of h. Simultaneously another body of mass 2m is thrown up vertically with such a velocity v that they collide at height h2. If the collision is perfectly inelastic, the velocity of combined mass at the time of collision with the ground will be
View SolutionA particle of mass 2m is dropped from a height 80 m above the ground. At the same time another particle of mass m is thrown vertically upwards from the ground with a speed of 40 m/s. If they collide head-on completely inelastically, the time taken for the combined mass to reach the ground, in units of second is:
View Solution
