There are two identical particles A and B. One is projected vertically upward with speed √2gh from ground and other is dropped from height h along the same vertical line. Collision between them is perfectly inelastic. Find time taken by them to reach the ground after collision in terms of √hg.
√32
√12
√3
√15
The correct Answer is:A
To solve the problem, we need to analyze the motion of two particles A and B before and after their collision. Here's a step-by-step breakdown of the solution:
Step 1: Analyze the motion of particle A
Particle A is projected vertically upward with an initial speed of vA=√2gh. The motion of A can be described by the following kinematic equation:
yA=vAt−12gt2
Where:
- yA is the height of particle A above the ground at time t.
- g is the acceleration due to gravity.
Step 2: Analyze the motion of particle B
Particle B is dropped from a height h with an initial speed of vB=0. The motion of B can be described by:
yB=h−12gt2
Where:
- yB is the height of particle B above the ground at time t.
Step 3: Find the time of collision
The particles collide when their heights are equal, i.e., yA=yB. Setting the equations equal gives:
√2ght−12gt2=h−12gt2
This simplifies to:
√2ght=h
From this, we can solve for t:
t=h√2gh=√h√2g
Step 4: Determine the height at which the collision occurs
Substituting t back into the equation for yA or yB to find the height at which they collide:
Using yA:
yA=√2gh(√h√2g)−12g(√h√2g)2
Calculating this gives:
yA=√2gh⋅√h√2g−12g⋅h2g=h−h4=3h4
Step 5: Find the velocity after collision
Since the collision is perfectly inelastic, both particles move together after the collision. To find their velocity just after the collision, we use the conservation of momentum:
mvA+mvB=(m+m)vf
Where:
- vA is the velocity of A just before the collision.
- vB is the velocity of B just before the collision.
- vf is the final velocity after the collision.
Calculating vA and vB just before the collision:
1. For particle A:
vA=√2g(3h4)=√3gh2
2. For particle B:
vB=√2gh−gt=√2gh−g⋅√h√2g=√2gh−gh√2g=√2gh−g√h√2
Using conservation of momentum:
m√3gh2+m(√2gh−g√h√2)=2mvf
This gives us the final velocity vf.
Step 6: Calculate the time to reach the ground after collision
After the collision, both particles fall from a height of 3h4 with an initial velocity vf. The time t′ taken to reach the ground can be calculated using:
h′=vft′+12gt′2
Where h′=3h4.
Final Result
After solving the equations, we find that the time taken by both particles to reach the ground after the collision is:
t′=√3h2g
Particle A is projected vertically upward with an initial speed of vA=√2gh. The motion of A can be described by the following kinematic equation:
- yA is the height of particle A above the ground at time t.
- g is the acceleration due to gravity.
Particle B is dropped from a height h with an initial speed of vB=0. The motion of B can be described by:
- yB is the height of particle B above the ground at time t.
The particles collide when their heights are equal, i.e., yA=yB. Setting the equations equal gives:
Substituting t back into the equation for yA or yB to find the height at which they collide:
Since the collision is perfectly inelastic, both particles move together after the collision. To find their velocity just after the collision, we use the conservation of momentum:
- vA is the velocity of A just before the collision.
- vB is the velocity of B just before the collision.
- vf is the final velocity after the collision.
vA=√2g(3h4)=√3gh2
vB=√2gh−gt=√2gh−g⋅√h√2g=√2gh−gh√2g=√2gh−g√h√2
After the collision, both particles fall from a height of 3h4 with an initial velocity vf. The time t′ taken to reach the ground can be calculated using:
After solving the equations, we find that the time taken by both particles to reach the ground after the collision is:
Topper's Solved these Questions
Similar Questions
Air offers a retardation of 6m/s2 to a particle. If it is projected vertically upwards with a speed of 96m/s from ground then the time of flight is : (g=10m/s2)
View SolutionA particle is projected vertically upwards from ground with velocity 10 m/s. Find the time taken by it to reach at the highest point ?
View Solution
Knowledge Check
A wooden ball and an iron ball are dropped from the same height h in vaccum. If their radii are the same then the time taken by then to reach the ground are
Aapproximately equalBexactly equalCnot equalDzero
A balloon rises from rest on the ground with constant acceleration g/8. A stone is dropped from the balloon when the balloon has risen to a height of (H). Find the time taken by the stone to reach the ground.
View SolutionA small particle of mass m is released from a height h on a large smooth sphere kept on a perfectly smooth surface as shown in the figure. Collision between particle and sphere is perfectly inelastic. Determine the velocities of particle and sphere after collision.
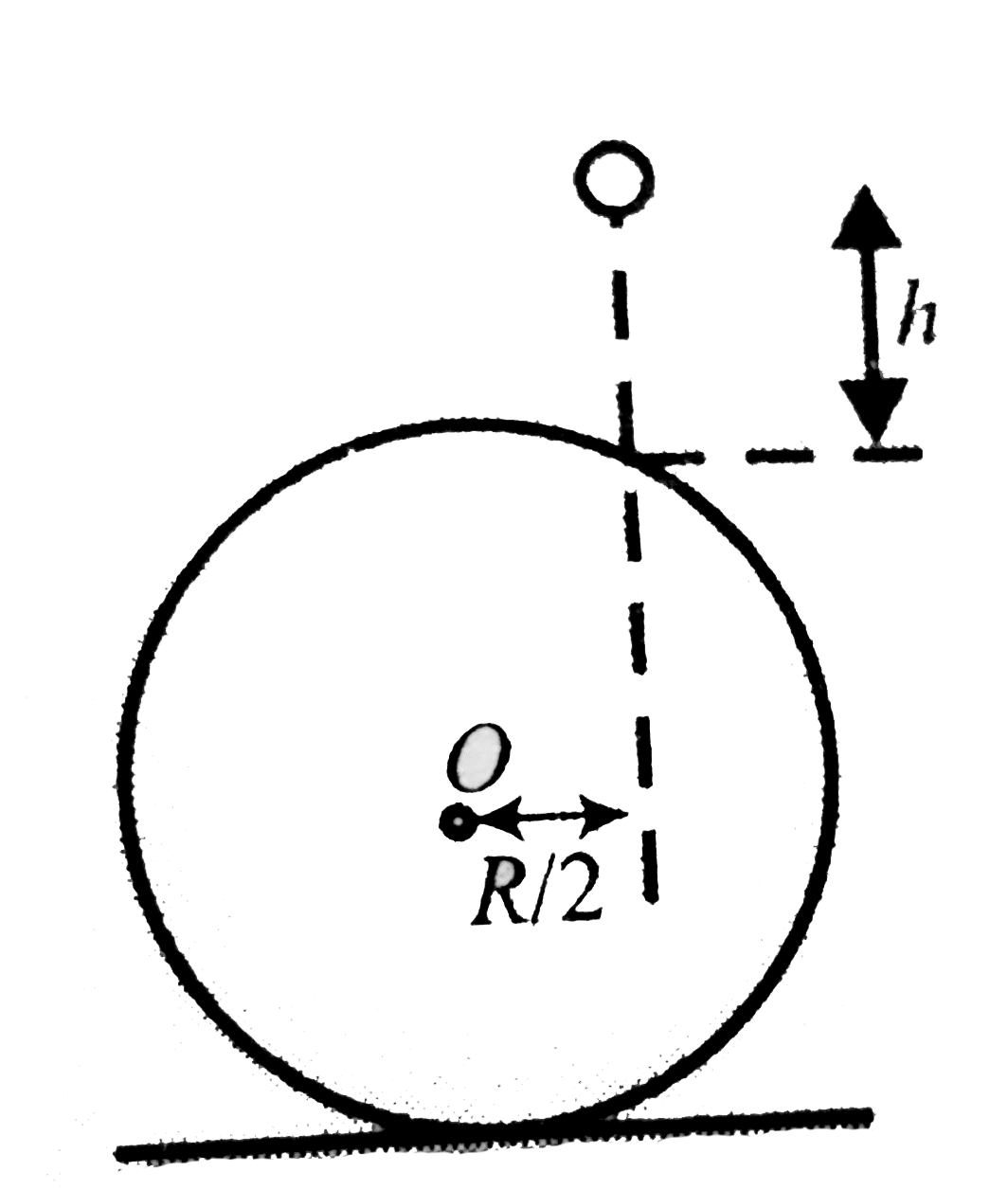
View SolutionA helicopter rises from rest on the ground vertically upwards with a constant acceleration g. A food packet is dropped from the helicopter when is at a height h. The time taken by the packet to reach the ground is close to [ g is the acceeration due to gravity] :
View SolutionTwo identical masses are as shown in figure. One is thrown upwards with velocity 20 m/s and another is just dropped simultaneously.
If the collision between them is elastic, find the time interval between their striking with ground
View SolutionAn iron ball and a wooden ball of the same radius are released from a height ‘ h ’ in vacuum. The time taken by both of them to reach the ground is
View SolutionA particle of mass m is dropped from a height h above the ground. At the same time another particle of mass 2m is thrown vertically upwards from the ground with a speed of √gh . If they collide head-on completely inelastically, the time taken for the combined mass to reach the ground, in units of √hg is:
View SolutionA particle of mass m is dropped from a height h above the ground. At the same time another particle of mass 2m is thrown vertically upwards from the ground with a speed of √gh . If they collide head-on completely inelastically, the time taken for the combined mass to reach the ground, in units of √hg is :
View Solution
