If the probability distribution of is as such
Then find the value of
To solve the problem, we need to find the conditional probability P(1<X<4|X≤2) given the probability distribution P(X) defined as follows:
X:0,1,2,3,4P(X):k,2k,3k,4k,5k
Step 1: Find the value of k
The sum of all probabilities must equal 1:
P(0)+P(1)+P(2)+P(3)+P(4)=k+2k+3k+4k+5k=15k=1
From this equation, we can solve for k:
k=115
Step 2: Calculate P(A) where A:1<X<4
The values of X that satisfy 1<X<4 are X=2,3. Thus:
P(A)=P(2)+P(3)=3k+4k=7k
Substituting the value of k:
P(A)=7⋅115=715
Step 3: Calculate P(B) where B:X≤2
The values of X that satisfy X≤2 are X=0,1,2. Thus:
P(B)=P(0)+P(1)+P(2)=k+2k+3k=6k
Substituting the value of k:
P(B)=6⋅115=615=25
Step 4: Calculate P(A∩B)
The intersection A∩B consists of the values that are both in A and B. The only value that satisfies both conditions is X=2:
P(A∩B)=P(2)=3k
Substituting the value of k:
P(A∩B)=3⋅115=315=15
Step 5: Calculate the conditional probability P(A|B)
Using the formula for conditional probability:
P(A|B)=P(A∩B)P(B)
Substituting the values we calculated:
P(A|B)=1525=12
Final Answer
Thus, the value of P(1<X<4|X≤2) is:
12
Topper's Solved these Questions
Similar Questions
Knowledge Check
Let probability distribution is [xi:12345pi:k22kk2k5k2] then value of p(x>2) is
A712B136C16D2336If X is a random -variable with distribution given below :
x:0123p(x):k3k3kk
The value of k and its variance areA1/8,22/27B1/8,23/27C1/8,24/27D1/8,3/4If the probability of a random variable X is a given below :
X=x:−2−10123P(X=x):12k152k310k
Then the value of k, is :A110B210C310D710
If the probability distribution of a random variable X is given by X=xi: 1 2 3 4 P(X=xi): 2k 4k 3k k Write the value of k .
View SolutionThe probability distribution of X is as follows:
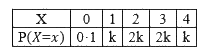
Find k and P [X<2].
View SolutionA random variable X has the following probability distribution: X=xi: 1 2 3 4 P(X=xi): k 2k 3k 4k Write the value of P(X≥3) .
View SolutionThe probability distribution of a random variable X is given below: X: 0 1 2 3 P(X):k k2 k4 k8 (i) Determine the value of k (ii) Determine P(X≤2)and P(X>2) (iii) Find P(X≤2)+P(X>2)
View SolutionA random variable X has following probability distribution
X=x123456P(X=x)K3K5K7K8KK
Then P(2≤X<5)= . . . .
View Solution
