A projectile fired at an angle 450 with horizontal. After 2s it acquires velocity of 20 m/s. Then the range of the projectile is.........
To solve the problem step by step, we will follow the principles of projectile motion.
Step 1: Understand the Problem
A projectile is fired at an angle of 45∘ with the horizontal. After 2 seconds, it has a velocity of 20m/s. We need to calculate the range of the projectile.
Step 2: Break Down the Velocity
The velocity of the projectile can be broken down into horizontal and vertical components.
Given:
- Angle θ=45∘
- Resultant velocity v=20m/s
The horizontal component of the velocity vx and the vertical component vy can be expressed as:
- vx=ucos(45∘)=u√2
- vy=usin(45∘)−gt=u√2−gt
Where g is the acceleration due to gravity (approximately 10m/s2) and t=2s.
Step 3: Use the Given Velocity
At t=2s, the vertical component of the velocity can be expressed as:
vy=u√2−g⋅t
Substituting the values:
vy=u√2−10⋅2
vy=u√2−20
Step 4: Apply the Pythagorean Theorem
Since the resultant velocity is given as 20m/s:
v2=v2x+v2y
Substituting the components:
202=(u√2)2+(u√2−20)2
Step 5: Expand and Simplify
Expanding the equation:
400=u22+(u√2−20)2
400=u22+(u22−20√2u+400)
Combining terms:
400=u2−20√2u+400
Step 6: Solve for Initial Velocity u
Subtract 400 from both sides:
0=u2−20√2u
Factoring out u:
u(u−20√2)=0
Thus, u=0 or u=20√2.
Step 7: Calculate the Range
Using the formula for the range of a projectile:
R=u2sin(2θ)g
Substituting θ=45∘ (where sin(90∘)=1):
R=(20√2)2⋅110
R=80010=80m
Final Answer
The range of the projectile is 80m.
---
A projectile is fired at an angle of 45∘ with the horizontal. After 2 seconds, it has a velocity of 20m/s. We need to calculate the range of the projectile.
The velocity of the projectile can be broken down into horizontal and vertical components.
- Angle θ=45∘
- Resultant velocity v=20m/s
- vx=ucos(45∘)=u√2
- vy=usin(45∘)−gt=u√2−gt
At t=2s, the vertical component of the velocity can be expressed as:
vy=u√2−g⋅t
Substituting the values:
vy=u√2−10⋅2
vy=u√2−20
Since the resultant velocity is given as 20m/s:
v2=v2x+v2y
Substituting the components:
202=(u√2)2+(u√2−20)2
Expanding the equation:
400=u22+(u√2−20)2
400=u22+(u22−20√2u+400)
Combining terms:
400=u2−20√2u+400
Subtract 400 from both sides:
0=u2−20√2u
Factoring out u:
u(u−20√2)=0
Thus, u=0 or u=20√2.
Using the formula for the range of a projectile:
R=u2sin(2θ)g
Substituting θ=45∘ (where sin(90∘)=1):
R=(20√2)2⋅110
R=80010=80m
The range of the projectile is 80m.
Topper's Solved these Questions
Similar Questions
Find the minimum velocity for which the horizontal range of a projectile is 39.2 m.
View SolutionA projectile shot at an angle of 450 above "the horizontal strikes a building 30m away at a point 15m above the point of projection.The magnitude and direction of velocity of projectile when it strikes the building?
View Solution
Knowledge Check
From the ground, a projectile is fired at an angle of 60 degree to the horizontal with a speed of 20 m s−1 The horizontal range of the projectile is
A10√3B20 mC20√3mD40√3Figure shows a projectile thrown with speed u = 20 m/s at an angle 30∘ with horizontal from the top of a building 40 m high. Then the horizontal range of projectile is
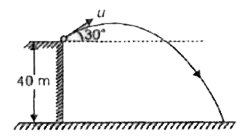 A20√3 mB40√3 mC40 mD20 m
A20√3 mB40√3 mC40 mD20 mA projectile is fired with velocity u making an angle θ with the horizontal. What is the angular momentum of the projectile at the highest point about the starting point ? (Given the mass of the projectile is m )
Amcosθ2gBmu2sin2θcosθ2gCmu3cos2θ2gDmu3sin∘θcosθ2g
A projectile is fired at an angle of 45∘ with the horizontal. Elevation angle of the projection at its highest point as seen from the point of projection is
View SolutionThe range of a projectile, when launched at an angle of 15∘ with the horizontal is 1.5 km. what is the range of the projectile, when launched at an angle of 45∘ to the horizontal with the same speed ?
View SolutionA missile is fired for maximum range with an initial velocity of 20m/s. If g=10m/s2, the range of the missile is
View SolutionIn case of a projectile fired at an angle equally inclined to the horizontal and vertical with velocity (u). The horizontal range is:-
View SolutionA projectile is fired at an angle of 30∘ with the horizontal such that the vertical component of its initial velocity is 80m/s. Find approximatly the velocity of the projectile at time T/4 where T is time of flight.
View Solution
