Wattless current flows in AC circuit then the circuit is
L only
RC only
LCR
R only
To solve the problem of determining which type of AC circuit allows for wattless current to flow, we need to analyze the conditions under which the power consumed in the circuit is zero.
1. Understanding Wattless Current:
- Wattless current refers to the current that does not do any work or produce power in the circuit. This occurs when the power factor (cos φ) is zero.
2. Power in AC Circuits:
- The power P in an AC circuit is given by the formula:
P=IRMS×VRMS×cosϕ
- Here, IRMS is the root mean square current, VRMS is the root mean square voltage, and ϕ is the phase difference between the current and voltage.
3. Condition for Wattless Current:
- For the power P to be zero (wattless current), we need:
cosϕ=0
- This occurs when ϕ=90∘.
4. Phase Difference in Circuits:
- In an AC circuit, the phase difference between current and voltage can be influenced by the type of components in the circuit:
- Resistor (R): ϕ=0∘ (current and voltage are in phase)
- Inductor (L): ϕ=90∘ (current lags voltage by 90 degrees)
- Capacitor (C): ϕ=−90∘ (current leads voltage by 90 degrees)
- RLC Circuit: The phase difference can vary depending on the values of R, L, and C.
5. Conclusion:
- Since wattless current occurs when the phase difference is 90∘, the only circuit type that satisfies this condition is an Inductive Circuit (L only). Therefore, the correct answer is:
Option A: L only
- Wattless current refers to the current that does not do any work or produce power in the circuit. This occurs when the power factor (cos φ) is zero.
- The power P in an AC circuit is given by the formula:
P=IRMS×VRMS×cosϕ
- Here, IRMS is the root mean square current, VRMS is the root mean square voltage, and ϕ is the phase difference between the current and voltage.
- For the power P to be zero (wattless current), we need:
cosϕ=0
- This occurs when ϕ=90∘.
- In an AC circuit, the phase difference between current and voltage can be influenced by the type of components in the circuit:
- Resistor (R): ϕ=0∘ (current and voltage are in phase)
- Inductor (L): ϕ=90∘ (current lags voltage by 90 degrees)
- Capacitor (C): ϕ=−90∘ (current leads voltage by 90 degrees)
- RLC Circuit: The phase difference can vary depending on the values of R, L, and C.
- Since wattless current occurs when the phase difference is 90∘, the only circuit type that satisfies this condition is an Inductive Circuit (L only). Therefore, the correct answer is:
Option A: L only
Topper's Solved these Questions
Similar Questions
Knowledge Check
In the figure shown, a current of 2 amperes flows in the circuit. The impedence of the circuit is-
 A170ΩB70ΩC130ΩD120Ω
A170ΩB70ΩC130ΩD120ΩIn an A.C. circuit the current
AAlways leads the voltageBAlways lags behind the voltageCIs always in phase with the voltageDMay lead or lag behind or be in phase with the voltageTotal current flowing through the circuit:
 A0.677 AB0.057 AC0.87 AD2.87 A
A0.677 AB0.057 AC0.87 AD2.87 A

Current flows through the above circuit when
View SolutionWhen a circuit element X is connected across on a.c. source of e.m.f. 220√2 volt, current of √2 A flows through it in phase with the voltage. When another element Y is connected across the same a.c. source, the same current flows through the circuit, but it leads the voltage by π/2 radian. Name the circuit element X and Y.
Find the current that flows in the circuit when series combination of X and Y is connected across the same source.
View SolutionIn the given circuit the AC source has ω=100rads−1. Considering the inductor and capacitor to be ideal, what will be the current I flowing through the circuit ?

View Solution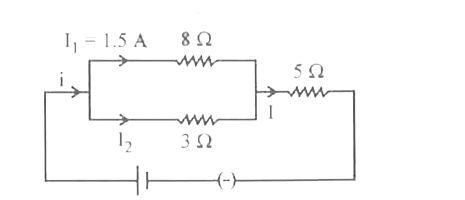
In the given circuit, the current in the 8Ω resistance is 1.5 A. What is the total current (I) flowing in the circuit ?
View SolutionWhat will be the phase difference between virtual voltage and virtual current, when the current in the circuit is wattless
View Solution

