For a particle moving in XY plane in UCM speed v and radius r the acceleration vector at any (r,θ) is ?
To find the acceleration vector of a particle moving in uniform circular motion (UCM) in the XY plane at any point defined by polar coordinates (r,θ), we can follow these steps:
1. Understanding Uniform Circular Motion (UCM):
- In UCM, a particle moves in a circular path with a constant speed v and a fixed radius r. The direction of the velocity vector changes continuously, but its magnitude remains constant.
2. Identify the Components of Acceleration:
- In UCM, the acceleration of the particle is entirely centripetal because the speed is constant. There is no tangential acceleration since the speed does not change.
- The centripetal acceleration ac is given by the formula:
ac=v2r
3. Direction of Centripetal Acceleration:
- The direction of centripetal acceleration is always towards the center of the circular path. If the particle is at an angle θ in polar coordinates, the acceleration vector will point radially inward.
4. Expressing Centripetal Acceleration in Cartesian Coordinates:
- In polar coordinates, the position of the particle can be expressed as:
x=rcos(θ),y=rsin(θ)
- The centripetal acceleration can be decomposed into its components using trigonometric functions:
- The x-component of the acceleration is:
ax=−accos(θ)=−v2rcos(θ)
- The y-component of the acceleration is:
ay=−acsin(θ)=−v2rsin(θ)
5. Combining Components into a Vector:
- The acceleration vector a can be expressed in terms of its components:
a=ax^i+ay^j=−v2rcos(θ)^i−v2rsin(θ)^j
6. Final Result:
- Therefore, the acceleration vector at any point (r,θ) for a particle in UCM is:
a=−v2rcos(θ)^i−v2rsin(θ)^j
- In UCM, a particle moves in a circular path with a constant speed v and a fixed radius r. The direction of the velocity vector changes continuously, but its magnitude remains constant.
- In UCM, the acceleration of the particle is entirely centripetal because the speed is constant. There is no tangential acceleration since the speed does not change.
- The centripetal acceleration ac is given by the formula:
ac=v2r
- The direction of centripetal acceleration is always towards the center of the circular path. If the particle is at an angle θ in polar coordinates, the acceleration vector will point radially inward.
- In polar coordinates, the position of the particle can be expressed as:
x=rcos(θ),y=rsin(θ)
- The centripetal acceleration can be decomposed into its components using trigonometric functions:
- The x-component of the acceleration is:
ax=−accos(θ)=−v2rcos(θ)
- The y-component of the acceleration is:
ay=−acsin(θ)=−v2rsin(θ)
- The acceleration vector a can be expressed in terms of its components:
a=ax^i+ay^j=−v2rcos(θ)^i−v2rsin(θ)^j
- Therefore, the acceleration vector at any point (r,θ) for a particle in UCM is:
a=−v2rcos(θ)^i−v2rsin(θ)^j
Topper's Solved these Questions
Similar Questions
Define centripetal acceleration. Derive anexpression for the centripetal acceleration of a particle moving with uniform speed v along a circular path of radius r. Discuss the direction of this acceleration
View SolutionIn Fig. a particle is moving in a circle of radius r centred at O with constant speed v. what is the change in velocity in moving from A to B ? Given ∠AOB=40∘.
View Solution
Knowledge Check
For a particle in uniform circular motion , the acceleration →a at a point p(R,θ) on the circle of radiu R is ( Here θ is measured from the x−aξs )
A−v2Rcosθˆi+v2RsinθˆjB−v2Rsinθˆi+v2RcosθˆjC−v2Rcosθˆi−v2RsinθˆjD−v2Rˆi+v2RˆjFor a particle in uniform circular motion the acceleration →a at a point P(R,θ) on the circle of radius R is : ( here θ is measured from the x- axis )
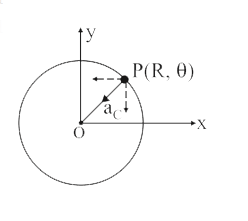 A−v2Rcosθˆi+v2RsinθˆjB−v2Rsinθˆi+v2RcosθˆjC−v2Rcosθhai−v2RsinθˆjDv2Rˆi+v2Rˆj
A−v2Rcosθˆi+v2RsinθˆjB−v2Rsinθˆi+v2RcosθˆjC−v2Rcosθhai−v2RsinθˆjDv2Rˆi+v2RˆjIf KE of the particle of mass m performing UCM in a circle of radius r is E. Find the acceleration of the particle
A2EmrB(2Emr)2C2EmrD4Emr
A particle is moving with a uniform speed v in a circular path of radius r with the centre at 0. When the particle moves from a point P to Q on the circle such that ∠POQ=θ , then the magnitude of the change in velocity is
View SolutionA particle is moving in a circular path of radius r under the action of a force F. If at an instant velocity of particle is v, and speed of particle is increasing, then
View SolutionIf a body is moving with a uniform speed v in a circle of radius 'r', then the angular acceleration of the body will be
View SolutionThe figure shows the total acceleration a=32ms−2 of a moving particle moving clockwise in a circle of radius R = 1 m . What are the centripetal acceleration a and speed of the particle at the given instant ?

View SolutionA particle starts moving at t = 0 in a circle of radius R=2m with constant angular acceleration of a−3rad/sec2. Initial angular speed of the particle is 1 rad/sec. At time t0 the angle between the acceleration vector and the velocity vector of the particle is 37∘.
What is the value of t0 ?
View Solution
