An aeroplane is flying horizontally with velocity 200 m/s when it is just above a canon. The canon fires a shell at a speed of 400 m/s at an angle of θ with horizontal. If shell hits the aeroplane then value of θ is
450
300
370
600
To solve the problem, we need to analyze the motion of the shell fired from the cannon and the motion of the airplane.
1. Identify the velocities:
- The airplane is flying horizontally with a velocity Va=200m/s.
- The shell is fired at a speed Vs=400m/s at an angle θ with the horizontal.
2. Resolve the shell's velocity into components:
- The horizontal component of the shell's velocity is given by:
Vsx=Vscosθ=400cosθ
- The vertical component of the shell's velocity is given by:
Vsy=Vssinθ=400sinθ
3. Set the horizontal components equal:
- For the shell to hit the airplane, the horizontal component of the shell's velocity must equal the airplane's velocity:
Vsx=Va
- Substituting the known values:
400cosθ=200
4. Solve for cosθ:
- Rearranging the equation gives:
cosθ=200400=12
5. Find θ:
- Taking the inverse cosine gives:
θ=cos−1(12)
- This results in:
θ=60∘
Final Answer:
The value of θ is 60∘.
---
- The airplane is flying horizontally with a velocity Va=200m/s.
- The shell is fired at a speed Vs=400m/s at an angle θ with the horizontal.
- The horizontal component of the shell's velocity is given by:
Vsx=Vscosθ=400cosθ
- The vertical component of the shell's velocity is given by:
Vsy=Vssinθ=400sinθ
- For the shell to hit the airplane, the horizontal component of the shell's velocity must equal the airplane's velocity:
Vsx=Va
- Substituting the known values:
400cosθ=200
- Rearranging the equation gives:
cosθ=200400=12
- Taking the inverse cosine gives:
θ=cos−1(12)
- This results in:
θ=60∘
The value of θ is 60∘.
Topper's Solved these Questions
Similar Questions
A fighter plane is flying horizontally at a height of 250m from ground with constant velocity of 500m/s. It passes exactly over a cannon which can fire a shell at any time in any direction with a speed of 100m/s. Find the duration of time for which the plane is in danger of being hit by a cannon shell.
View SolutionAn aircraft is .flying. horizontally with a constant vefocity =200m/s at a height =1km above groun At the momement shown, a bomb is released from the aircraft and the cannon-gun below fires a shell with initial speed =200m/s , at some angle θ For what value of θ will the projectile shell destroy the bomb in mid-air? If the value of θ is 533 , find the minimum distance between the bomb and the shell as they fly past each other. Take sin53∘=4/5
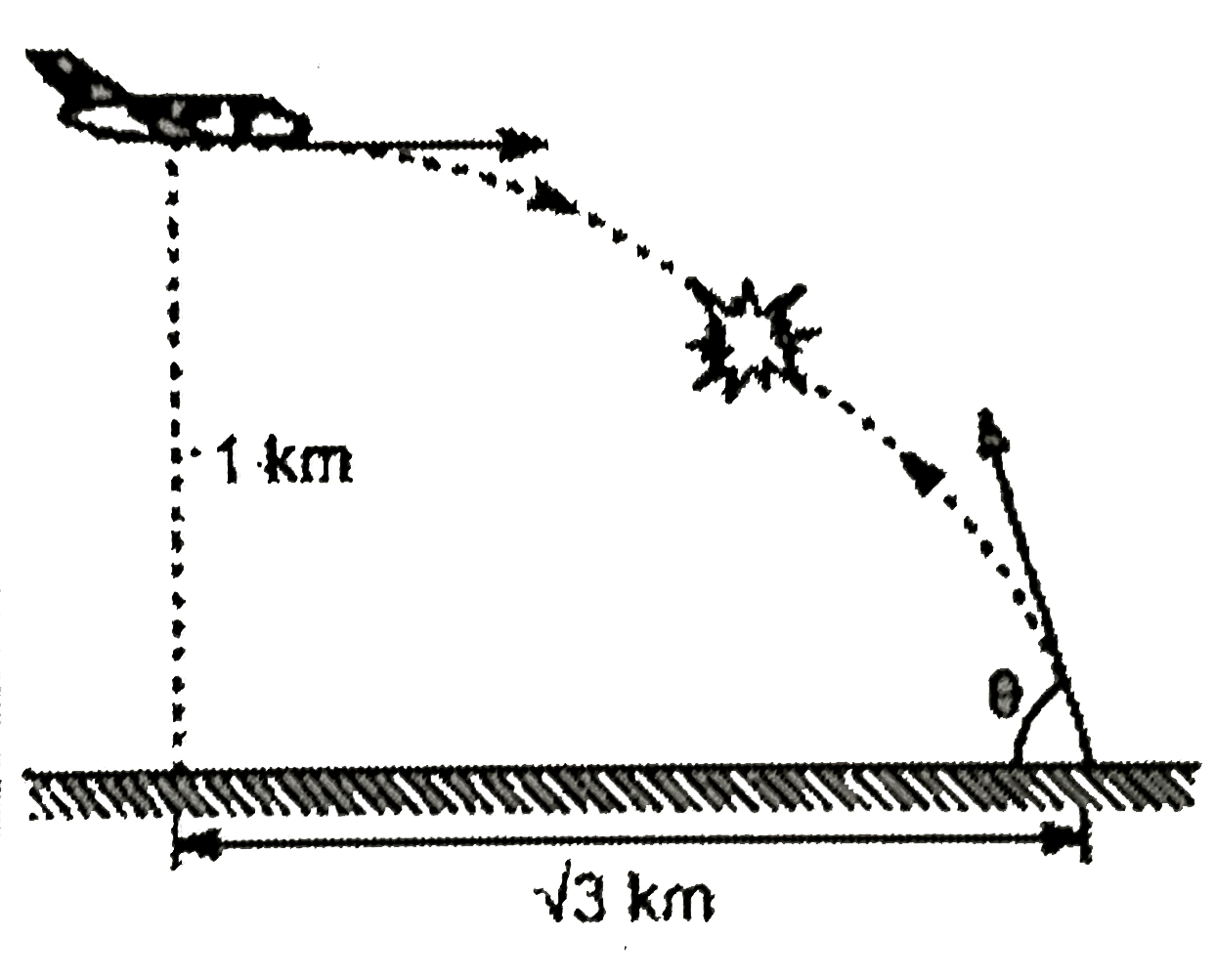
View Solution
Knowledge Check
An aeroplane is flying horizontally with a velocity of 720 km/h at an altitude of 490 m. When it is just vertically above the target a bomb is dropped from it. How far horizontally it missed the target?
A1000mB2000mC100mD200mTwo enemy guns are placed at A and B at 10√3km apart horizontally . A shell is fired from A horizontally with velocity 10m/s. At the same time a shell of double the mass of shell at A is fired from B at an angle 60∘ with horizontal towards A with the same magnitude of initial velocity as that of A. Moving in the same vertical plane, two shells collide in air while sticking to each other and falling at the depest point of the valley C (neglect air resistance).

Find the time of collision of the two shells (in sec).A200√3B20√3C2×103√3D2×104√3Two enemy guns are placed at A and B at 10√3km apart horizontally . A shell is fired from A horizontally with velocity 10m/s. At the same time a shell of double the mass of shell at A is fired from B at an angle 60∘ with horizontal towards A with the same magnitude of initial velocity as that of A. Moving in the same vertical plane, two shells collide in air while sticking to each other and falling at the depest point of the valley C (neglect air resistance).

Find the magnitude of horizontal component of the displacement vector (→BC) (inkm).A11.55B5.77C10.98D6.12
A shell is fired into ait at an angle θ with the horizontal form the ground. On reaching the maximum height
View SolutionA stone is thrown with a velocity v at an angle θ with the horizontal.Its speed when it makes an angle β with the horizontal is
View SolutionAn aeroplane moving horizontally with a speed of 180km/hr. drops a food packet while flying at a height of 490m. The horizontal range of the packet is:-
View SolutionA man running with velocity 3m/s finds that raindrops are hitting him vertically with a speed of 4m/s.
Raindrops are falling at an angle θ with the vertical. Value of θ is
View SolutionAn aeroplane is flying at a height of 1960 m in horizontal direction with a velocity of 360 km/hr. When it is vertically above the point. A on the ground, it drops a bomb. The bomb strikes a point B on the ground, then the time taken by the bomb to reach the ground is-
View Solution
