A capacitor C1 is charged to a potential difference V. The charging battery is then removed and the capacitor is connected to an uncharged capacitor C2. The potential difference across the combination is
VC1C1+C2
VC2C1+C2
VC1C2C1+C2
VC1+C2
To solve the problem, we will analyze the situation step by step.
Step 1: Understand the Initial Conditions
We have a capacitor C1 that is charged to a potential difference V. The charge Q on the capacitor can be calculated using the formula:
Q=C1⋅V
Hint: Remember that the charge on a capacitor is given by the product of its capacitance and the voltage across it.
Step 2: Disconnect the Battery
Once the battery is removed, the charge Q on capacitor C1 remains constant because there is no path for charge to flow away from it.
Hint: The charge on a capacitor remains constant when it is isolated from the circuit.
Step 3: Connect to the Uncharged Capacitor
Now, we connect the charged capacitor C1 to an uncharged capacitor C2. Initially, the potential difference across C2 is 0 because it is uncharged.
Hint: An uncharged capacitor has no voltage across it, which means its initial voltage V2=0.
Step 4: Analyze the Final Configuration
After connecting C1 and C2, the total charge Q will redistribute between the two capacitors. The final potential difference across the combination can be denoted as V.
The total charge after connecting the capacitors can be expressed as:
Q=C1⋅V+C2⋅V
Since the charge is conserved, we can set this equal to the initial charge on C1:
C1⋅V+C2⋅V=C1⋅V
Step 5: Factor Out the Common Terms
Factoring out V from the left side gives us:
V(C1+C2)=C1⋅V
Step 6: Solve for the Final Voltage
Now, we can solve for V:
V=C1⋅VC1+C2
This equation gives us the potential difference across the combination of capacitors after they are connected.
Final Answer:
V=C1⋅VC1+C2
Summary
The potential difference across the combination of the two capacitors after connecting them is given by the formula:
V=C1⋅VC1+C2
We have a capacitor C1 that is charged to a potential difference V. The charge Q on the capacitor can be calculated using the formula:
Q=C1⋅V
Once the battery is removed, the charge Q on capacitor C1 remains constant because there is no path for charge to flow away from it.
Now, we connect the charged capacitor C1 to an uncharged capacitor C2. Initially, the potential difference across C2 is 0 because it is uncharged.
After connecting C1 and C2, the total charge Q will redistribute between the two capacitors. The final potential difference across the combination can be denoted as V.
Q=C1⋅V+C2⋅V
C1⋅V+C2⋅V=C1⋅V
Factoring out V from the left side gives us:
V(C1+C2)=C1⋅V
Now, we can solve for V:
V=C1⋅VC1+C2
V=C1⋅VC1+C2
The potential difference across the combination of the two capacitors after connecting them is given by the formula:
V=C1⋅VC1+C2
Topper's Solved these Questions
Similar Questions
A μF capacitor C1 is charged to V0=120V. The charging battery is then removed and the capacitor is connected in parallel to an uncharged +4μF capacitor C2.
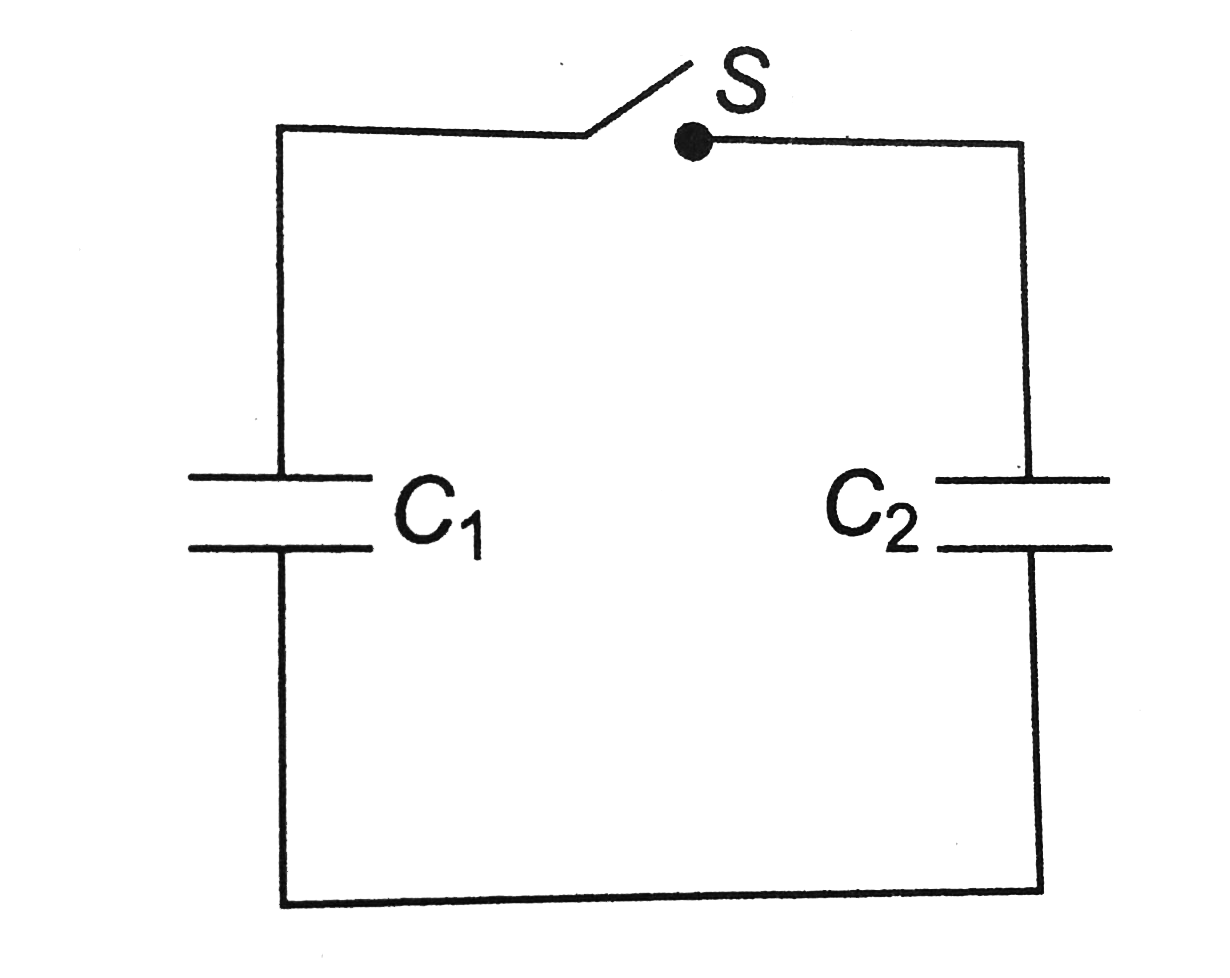
(a) what is the potential difference V across the combination?
(b) what is the stored energy before and after the switch S is closed?
View SolutionA 100pF capacitor is charged to a potential difference of 80.0V and the charging battery is disconnected. The capacitor is then connected in parallel with a second capacitor. If the potential difference across the first capacitor drops to 35.0 V what is the capacitance of this second capacitor?
View Solution
Knowledge Check
A capacitor of capacitance C is charged to a potential difference V0. The charged battery is disconnected and the capacitor is connected to a capacitor of unknown capacitance Cx. The potential difference across the combination is V. The value of Cx should be
AC(V0−V)VBC(V−V0)VCCVV0DCV0VA capacitor C1 is charged to a p.d.V. The charging battery is then removed and the capacitor is connected to an uncharged capacitor C2. The final p.d. across the combination is
AVC1C1+C2BVC2C1+C2CVC1C2C1+C2DVC1+C2A capacitor or capacitance C1 is charge to a potential V and then connected in parallel to an uncharged capacitor of capacitance C2. The fianl potential difference across each capacitor will be
AC1VC1+C2BC2VC1+C2C1+C2C1D1−C2C1
A 2μF capacitor C1 is first charged to a potential difference of 10 V using a battery. Then the battery is removed and the capacitor is connected to an uncharged capacitor C2 of 8μF. The charge in C2 on equilibrium condition is _______μC. (Round off to the Nearest Integer)
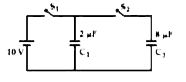
View SolutionFind charge on each capacitor and potential difference across each capacitor .

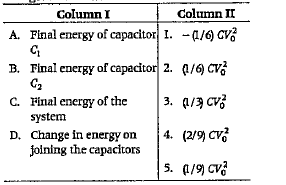
View SolutionA capacitor C1 of capacitance C is charged to a potential difference V0. The terminal of the charged capacitor are then connected to an uncharged capacitor C2of capacitance C/2. Match the entries of Column I with the entries of Column II and choose the correct option from the codes given below.
View SolutionA capacitor is charged by a cell of emf E the charging battery is then removed. If an identical capacitor is now inserted in the circuit in parallel with the previous capacitor, the potential difference across the new capacitor is
View SolutionAn uncharged capacitor is connected to a battery. On charging the capacitor
View Solution
