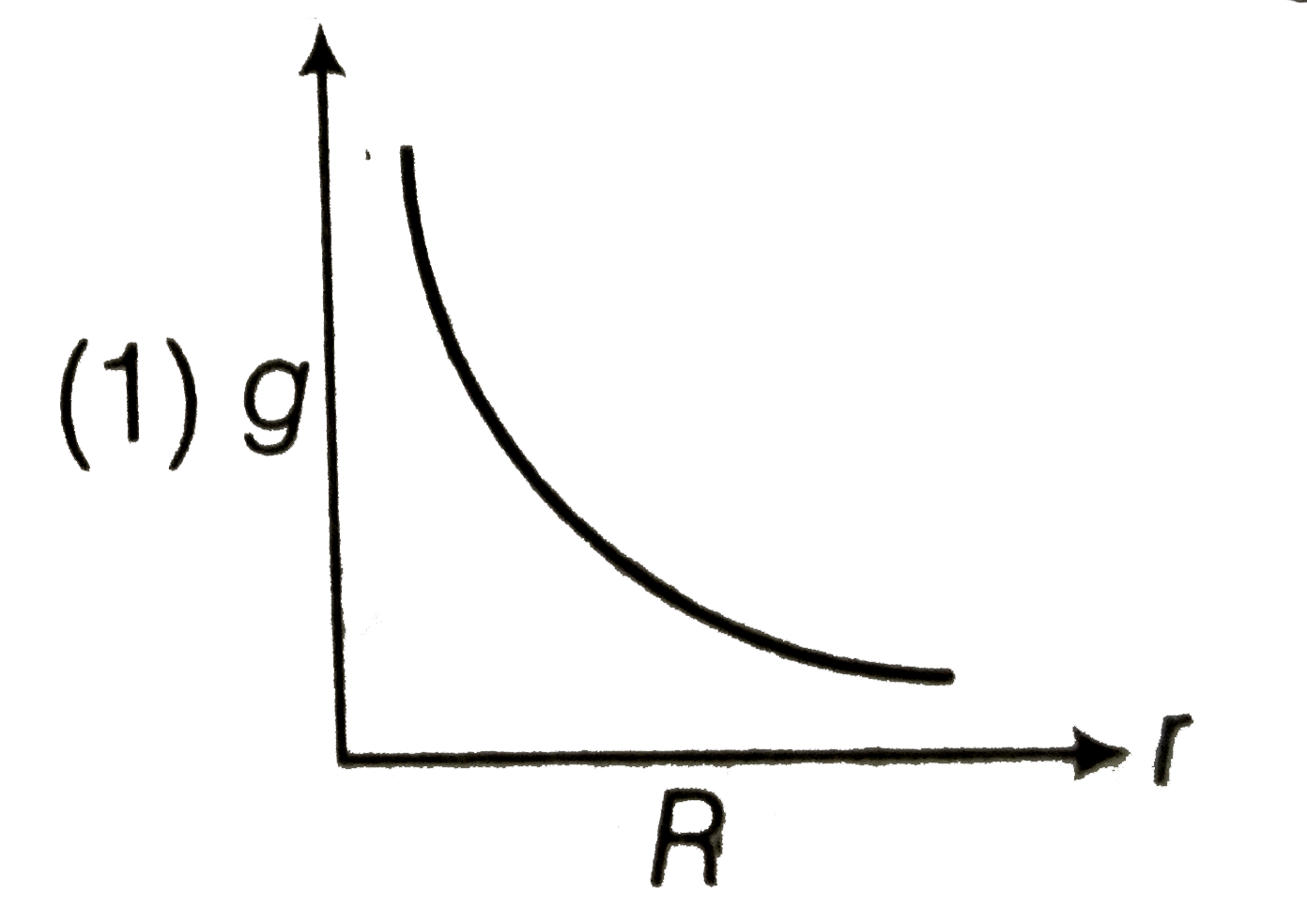
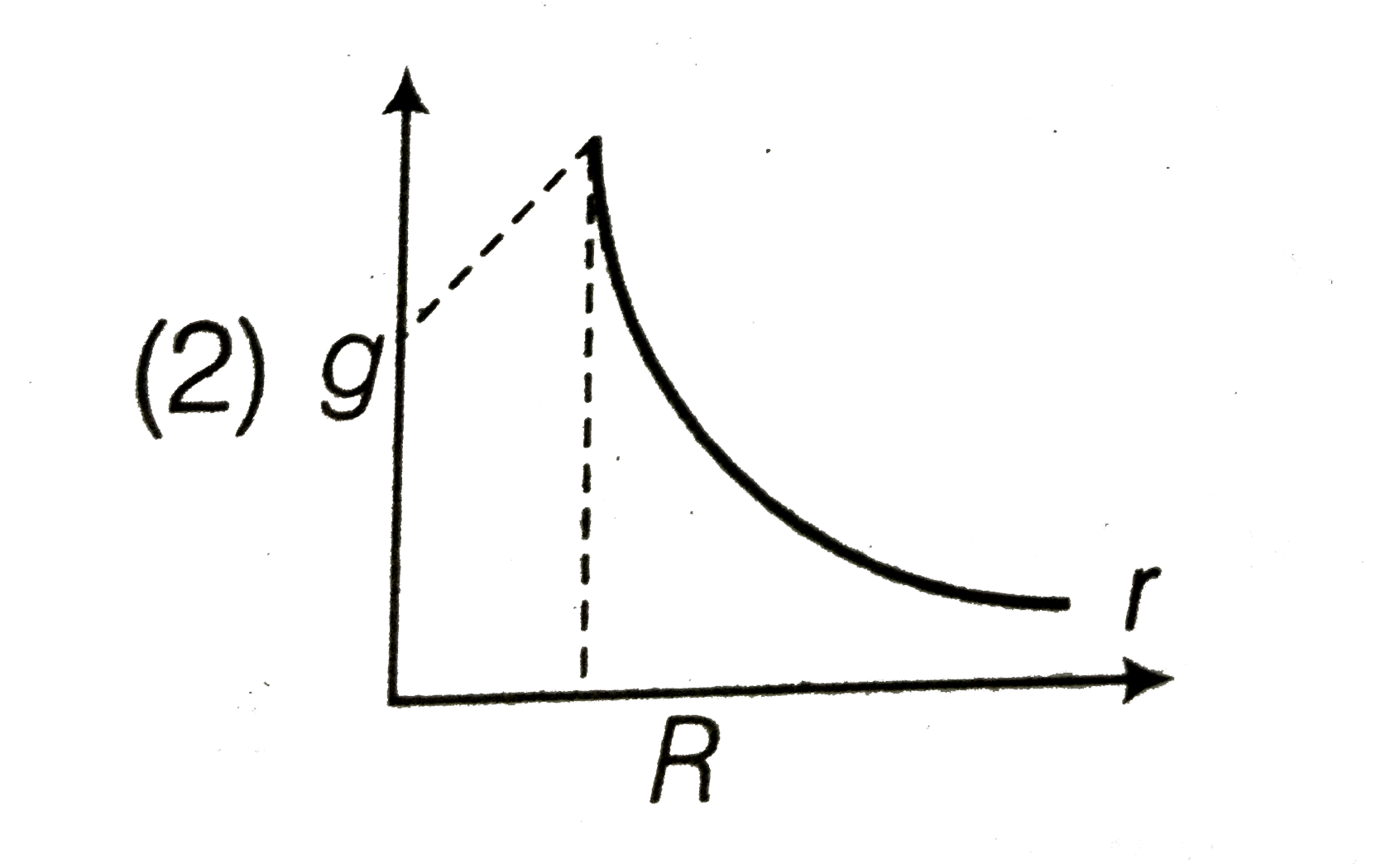
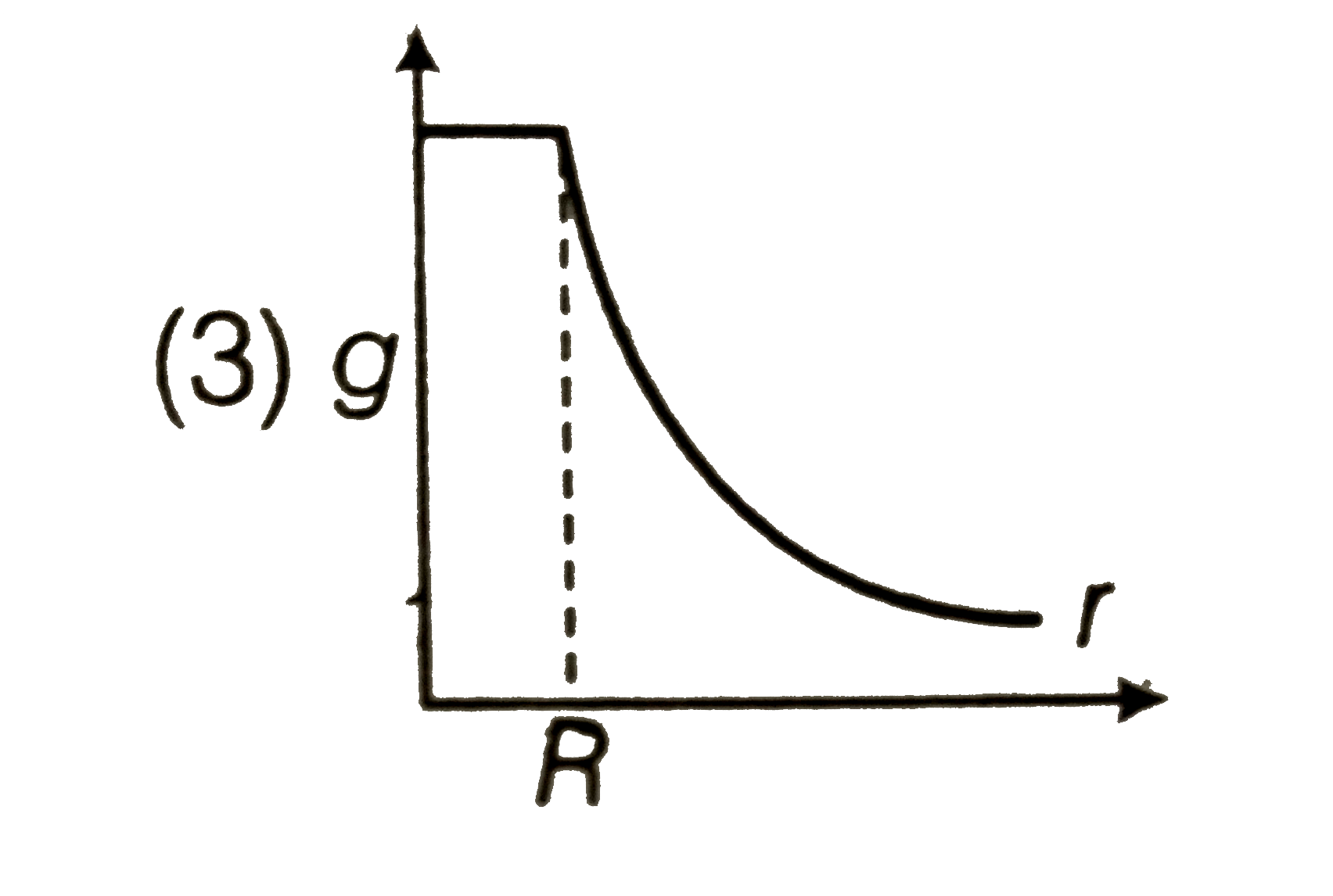
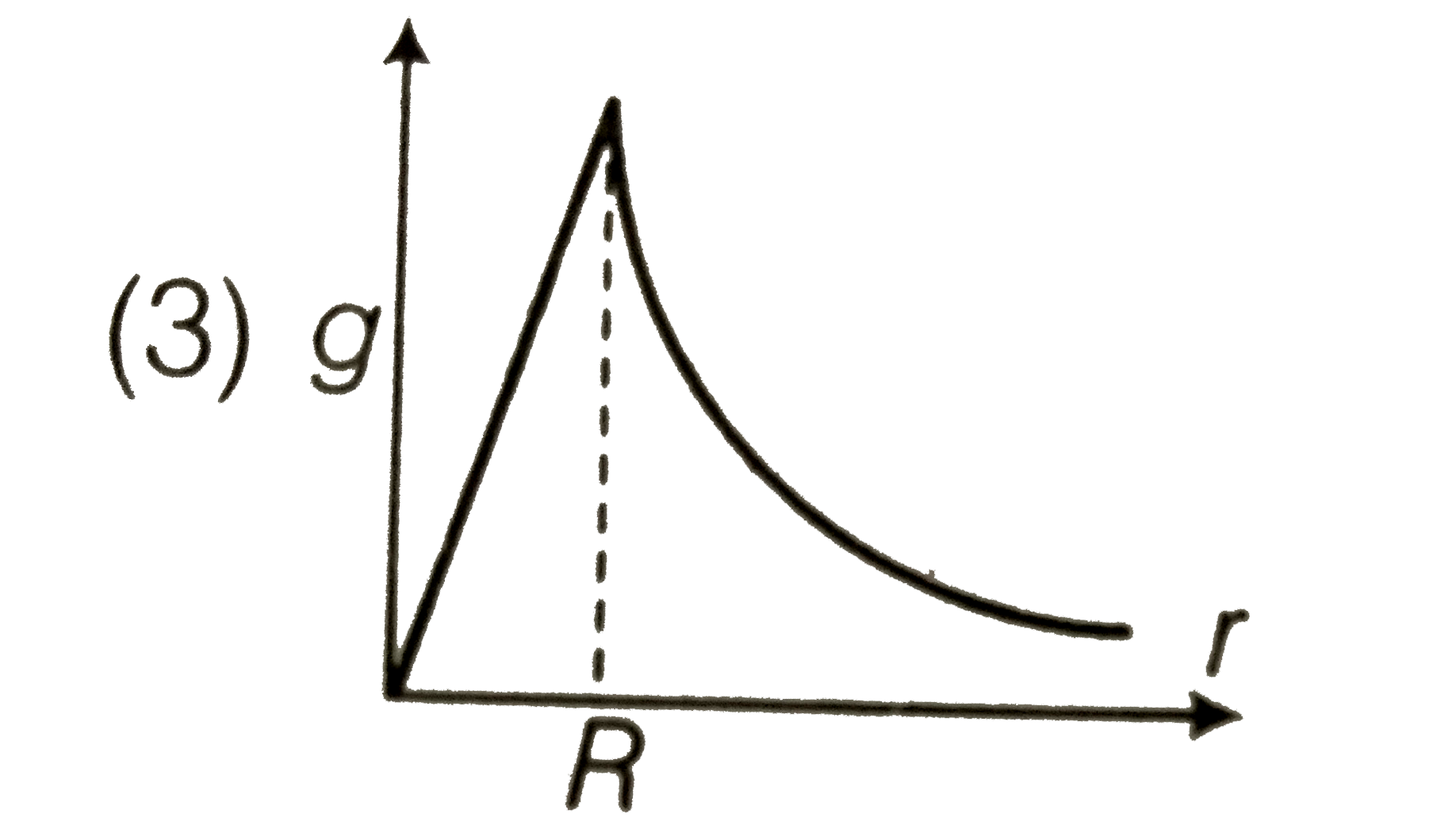
The dependence of acceleration due to gravity g on the distance r from the centre of earth. Correct figure is
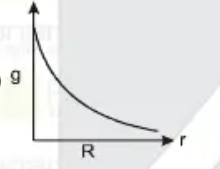
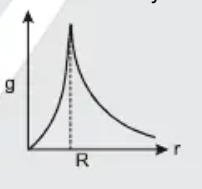
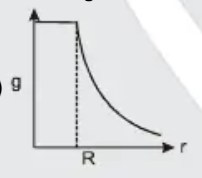

To solve the problem of how the acceleration due to gravity g depends on the distance r from the center of the Earth, we can break it down into two main regions: inside the Earth and outside the Earth.
1. Understanding the Regions:
- We need to consider two cases:
- When r<R (inside the Earth)
- When r≥R (outside the Earth)
- Here, R is the radius of the Earth.
2. Case 1: Inside the Earth (r<R):
- According to the shell theorem, the gravitational force inside a uniform spherical shell is zero. Therefore, only the mass that is at a distance less than r contributes to the gravitational field.
- The gravitational field g′ at a distance r from the center is given by:
g′=GM′r2
where M′ is the mass enclosed within radius r.
- The mass M′ can be expressed as:
M′=ρ⋅43πr3
where ρ is the density of the Earth (assumed constant).
- The total mass of the Earth M can be expressed as:
M=ρ⋅43πR3
- Thus, we can relate g′ to g (the acceleration due to gravity at the surface):
g′=GM′r2=G(ρ⋅43πr3)r2=43πGρr
- Since g=GMR2, we can express g′ in terms of g:
g′=gR3r
- This shows that g′ is directly proportional to r when r<R.
3. Case 2: Outside the Earth (r≥R):
- For distances greater than the Earth's radius, the gravitational acceleration g′ is given by:
g′=GMr2
- Here, g′ is inversely proportional to the square of the distance r:
g′∝1r2
4. Graphical Representation:
- For r<R, the graph of g′ versus r will be a straight line passing through the origin (linear relationship).
- For r≥R, the graph will show a hyperbolic decrease (inverse square relationship).
- The correct graph will show a linear increase for r<R and a decrease for r≥R.
Conclusion:
The correct graph depicting the dependence of acceleration due to gravity g on the distance r from the center of the Earth will show a linear increase for r<R and a hyperbolic decrease for r≥R.
- We need to consider two cases:
- When r<R (inside the Earth)
- When r≥R (outside the Earth)
- Here, R is the radius of the Earth.
- According to the shell theorem, the gravitational force inside a uniform spherical shell is zero. Therefore, only the mass that is at a distance less than r contributes to the gravitational field.
- The gravitational field g′ at a distance r from the center is given by:
g′=GM′r2
where M′ is the mass enclosed within radius r.
- The mass M′ can be expressed as:
M′=ρ⋅43πr3
where ρ is the density of the Earth (assumed constant).
- The total mass of the Earth M can be expressed as:
M=ρ⋅43πR3
- Thus, we can relate g′ to g (the acceleration due to gravity at the surface):
g′=GM′r2=G(ρ⋅43πr3)r2=43πGρr
- Since g=GMR2, we can express g′ in terms of g:
g′=gR3r
- This shows that g′ is directly proportional to r when r<R.
- For distances greater than the Earth's radius, the gravitational acceleration g′ is given by:
g′=GMr2
- Here, g′ is inversely proportional to the square of the distance r:
g′∝1r2
- For r<R, the graph of g′ versus r will be a straight line passing through the origin (linear relationship).
- For r≥R, the graph will show a hyperbolic decrease (inverse square relationship).
- The correct graph will show a linear increase for r<R and a decrease for r≥R.
The correct graph depicting the dependence of acceleration due to gravity g on the distance r from the center of the Earth will show a linear increase for r<R and a hyperbolic decrease for r≥R.
Topper's Solved these Questions
Similar Questions
Knowledge Check
The dependence of acceleration due to gravity g on the distance r from the centre of the earth, assumed to br a sphere of radius R of uniform density is as shoen in Fig. below:

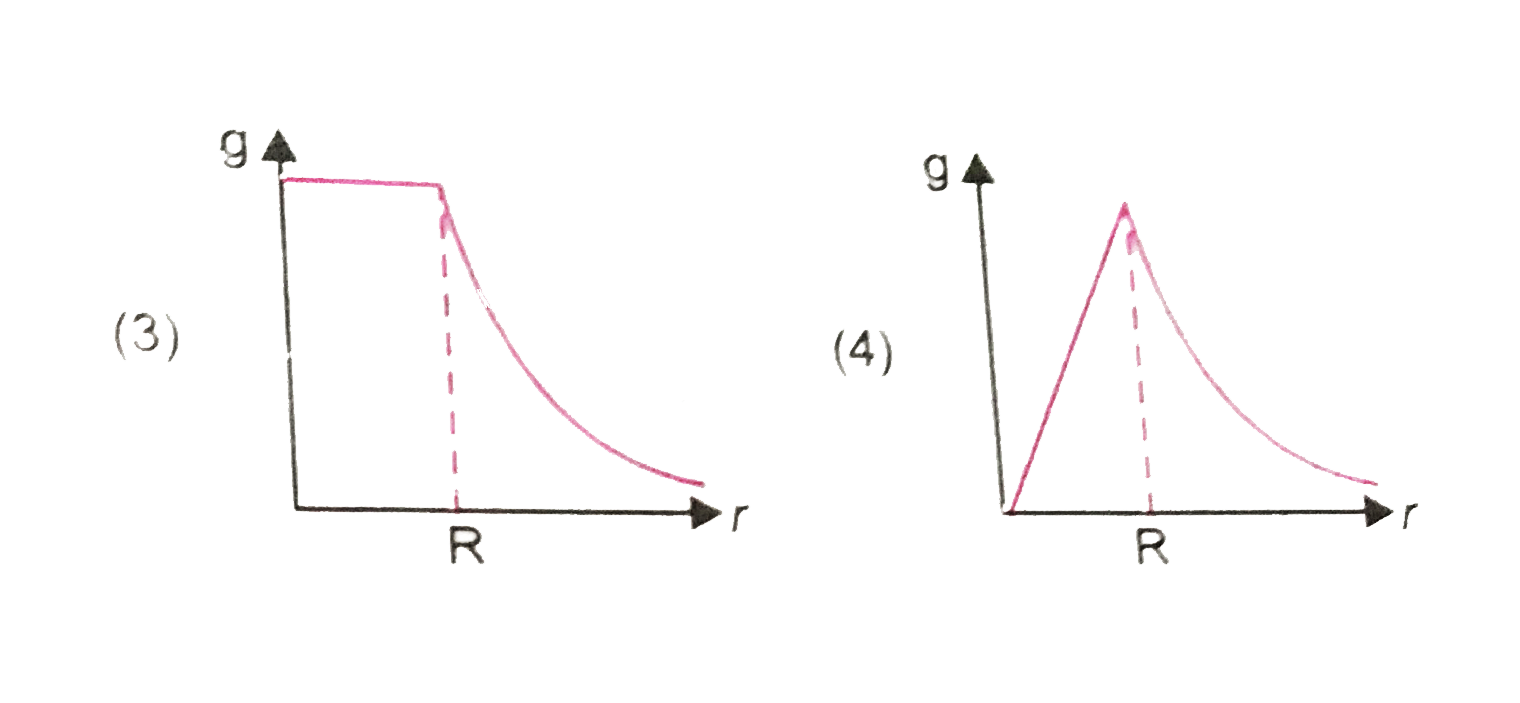
The correct figure isA(4)B(1)C(2)D(3)The value of acceleration due to gravity depends on
ApressureBaccelerationCgravitational forceDnone of theseIf g denotes the value of acceleration due to gravity at a point distance r from the centre of earth of radius R. If r<R, then
Ag∝r2Bg∝rCg∝1/r2Dg∝1/r
Find the acceleration due to gravity at a distance of 20000 kg from the centre of the earth.
View SolutionFind the acceleration due to gravity at a distance of 20000 km from the centre of the earth.
View SolutionIf earth is assumed to be a sphere of uniform density then plot a graph between acceleration due to gravity (g) and distance from the centre of earth.
View SolutionThe graph showing acceleration due to gravity of the earth from the center of the earth is
View SolutionThe value of acceleration due to gravity on earth depends on
View Solution