Two blocks of mass 10kg, 30kg coordinate (0,0) and at (x,0). A block of 10kg is moved a distance of 6cm towards 30kg. Find the distance moved by mass of 30kg block to keep centre of mass at same place.
1cm
2cm
4cm
5cm
To solve the problem, we need to find the distance moved by the 30 kg block to keep the center of mass of the system unchanged when the 10 kg block is moved 6 cm towards it.
1. Identify the Initial Positions:
- Let the position of the 10 kg block (m1) be at the origin (0, 0).
- Let the position of the 30 kg block (m2) be at (x, 0).
2. Calculate the Initial Center of Mass (CM):
The formula for the center of mass (CM) of two blocks is given by:
CM=m1⋅x1+m2⋅x2m1+m2
Substituting the values:
CM=10⋅0+30⋅x10+30=30x40=3x4
3. Determine the New Position of the 10 kg Block:
The 10 kg block is moved 6 cm towards the 30 kg block. Therefore, its new position (x1) becomes:
x1=0+0.06=0.06 m
4. Calculate the New Center of Mass:
After the 10 kg block is moved, the new center of mass (CM') can be calculated as:
CM′=10⋅0.06+30⋅x210+30
where x2 is the new position of the 30 kg block after it has moved a distance d.
5. Set the Centers of Mass Equal:
Since we want the center of mass to remain unchanged, we set the initial center of mass equal to the new center of mass:
3x4=10⋅0.06+30⋅(x+d)40
6. Solve for the Distance Moved by the 30 kg Block:
Rearranging the equation:
3x=10⋅0.06+30(x+d)
3x=0.6+30x+30d
3x−30x=0.6+30d
−27x=0.6+30d
30d=−27x−0.6
d=−27x−0.630
7. Substituting the Value of x:
We need to find the distance d that the 30 kg block moves. Since we know that the 10 kg block moved 6 cm (0.06 m), we can use the relation derived from the center of mass:
m1⋅x1=m2⋅x2
where x2 is the distance moved by the 30 kg block. Thus:
10⋅0.06=30⋅d
0.6=30d
d=0.630=0.02 m=2 cm
Final Answer:
The distance moved by the 30 kg block to keep the center of mass at the same place is 2 cm.
- Let the position of the 10 kg block (m1) be at the origin (0, 0).
- Let the position of the 30 kg block (m2) be at (x, 0).
The formula for the center of mass (CM) of two blocks is given by:
CM=m1⋅x1+m2⋅x2m1+m2
Substituting the values:
CM=10⋅0+30⋅x10+30=30x40=3x4
The 10 kg block is moved 6 cm towards the 30 kg block. Therefore, its new position (x1) becomes:
x1=0+0.06=0.06 m
After the 10 kg block is moved, the new center of mass (CM') can be calculated as:
CM′=10⋅0.06+30⋅x210+30
where x2 is the new position of the 30 kg block after it has moved a distance d.
Since we want the center of mass to remain unchanged, we set the initial center of mass equal to the new center of mass:
3x4=10⋅0.06+30⋅(x+d)40
Rearranging the equation:
3x=10⋅0.06+30(x+d)
3x=0.6+30x+30d
3x−30x=0.6+30d
−27x=0.6+30d
30d=−27x−0.6
d=−27x−0.630
We need to find the distance d that the 30 kg block moves. Since we know that the 10 kg block moved 6 cm (0.06 m), we can use the relation derived from the center of mass:
m1⋅x1=m2⋅x2
where x2 is the distance moved by the 30 kg block. Thus:
10⋅0.06=30⋅d
0.6=30d
d=0.630=0.02 m=2 cm
The distance moved by the 30 kg block to keep the center of mass at the same place is 2 cm.
Topper's Solved these Questions
Similar Questions
Two blocks of masses 10kg and 30kg are placed on X-axis. The first mass is moved on the axis by a distance of 2cm right. By what distance should the second mass be moved to keep the position of centre of mass unchanged.
View SolutionTwo blocks of masses 10 kg and 30 kg are placed along a vertical line. The first block is raised through a height of 7 cm. By what distance should the second mass be moved to raise the centre of mass by 1 cm?
View Solution
Knowledge Check
Initially spring is in its natural length . The block of mass 3kg in contact with rigid wall . The block of mass 1kg is pushed through a distance 4cm towards the wall and then released. The velocity of the center of mass when the block of mass 3kg breaks off the wall is (k=100N/m)
 A0.1m/sB0.2m/sC0.3m/sD0.4m/s
A0.1m/sB0.2m/sC0.3m/sD0.4m/sConsider a system of two particles having masses 2kg and 5 kg the particle of mass 2 kg is pushed towards the centre of mass of particles through a distance 5 m,by what distance would particle of mass 5kg move so as to keep the centre of mass of particles at the original position?
A2 mB12.5mC8mD5mTwo blocks of masses of 40 kg and 30 kg are connected by a weightless string passing over a frictionless pulley as shown in the figure.
 A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2
A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2
Two bocks of masses 10 g and 20 kg are placed on the X-axis. The first mass is moved on the axis by a distance of 2 cm. By what distance should the second mass be moved to keep the position of the centre of mass unchanged?
View SolutionTwo particles of mass 2 kg and 4 kg lie on the same line. If 4 kg is displaced rightwards by 5m then by what distance 2 kg should be move for which centre of mass will remain at the same position
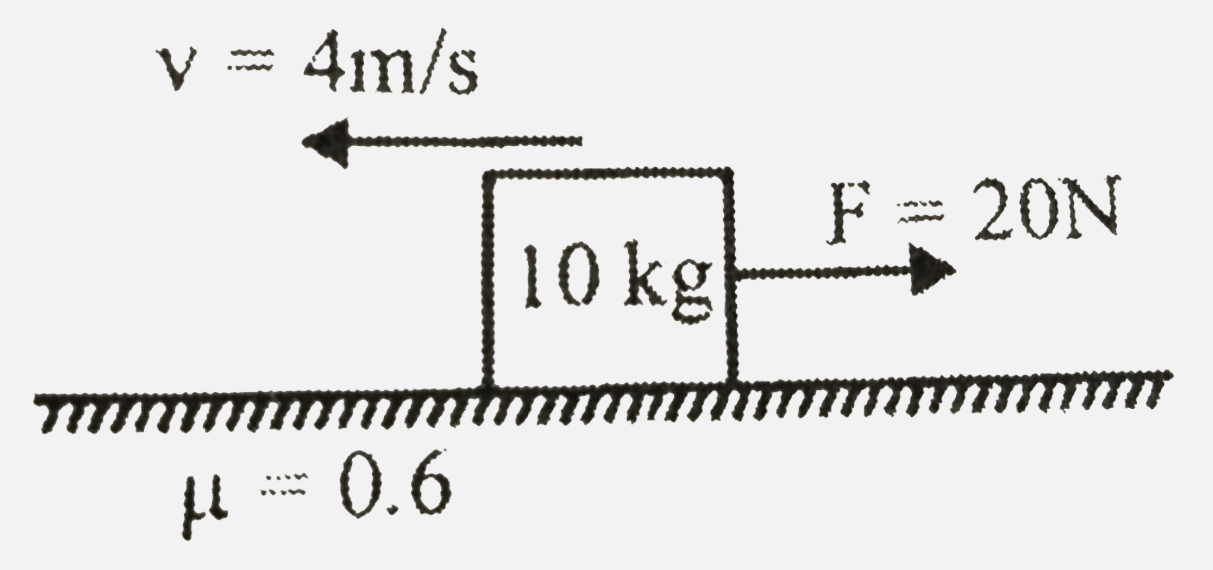
View SolutionA block of mass 10 kg is moving on a rough surface as shown in figure. The frictional force acting on block is :-
View SolutionA plank of mass 10kg rests on a smooth horizontal surface. Two blocks A and B of masses mA=2kgandmB=1kg lies at a distance of 3m on the plank as shown in the distance of 3m on the plank as shown in the figure. The friction coefficient between the blocks and plank are μA=0.3andμB=0.1. Now a force F = 15 N is applied to the plank in horizontal direction. Find the time after which block A collides with B.
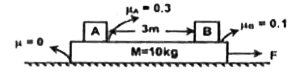
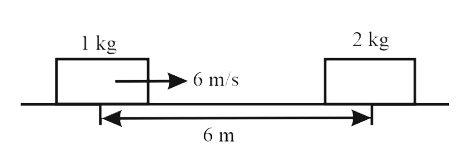
View SolutionA block of mass 1 kg is pushed towards another block of mass 2 kg from a 6 m distance as shown in the figure. If just after the collision, the velocity of 2 kg block is 4ms−1, then
View Solution
