In an experiment of potentiometer, if R= 8 ohm then null point AC is equal to 3 m and where R= 4 ohm, then AC is 2 m. find the value of internal resistance r.
To solve the problem of finding the internal resistance r in a potentiometer experiment, we can follow these steps:
Step 1: Understand the given data
We have two scenarios:
1. When R1=8Ω, the null point AC=3m.
2. When R2=4Ω, the null point AC=2m.
Step 2: Set up the relationship
The potential gradient K for the potentiometer is given by:
K=EL
where E is the electromotive force (emf) and L is the length of the wire.
The potential difference across the length L1 and L2 can be expressed as:
V1=K⋅L1
V2=K⋅L2
Since the potential difference across the null points must be equal to the potential drop across the resistors, we can write:
K⋅L1=I1⋅(R1+r)
K⋅L2=I2⋅(R2+r)
Step 3: Relate the currents
The current I through the circuit can be expressed using Ohm's law:
I=ER+r
Thus, we can express I1 and I2 as:
I1=ER1+r
I2=ER2+r
Step 4: Substitute the currents into the equations
Substituting I1 and I2 into the equations gives:
K⋅L1=ER1+r⋅(R1+r)
K⋅L2=ER2+r⋅(R2+r)
Step 5: Set up the ratio
From the two equations, we can set up a ratio:
L1L2=R1+rR2+r
Step 6: Substitute known values
Substituting the known values:
32=8+r4+r
Step 7: Cross-multiply and solve for r
Cross-multiplying gives:
3(4+r)=2(8+r)
Expanding both sides:
12+3r=16+2r
Rearranging gives:
3r−2r=16−12
r=4Ω
Conclusion
The internal resistance r is 4Ω.
We have two scenarios:
1. When R1=8Ω, the null point AC=3m.
2. When R2=4Ω, the null point AC=2m.
The potential gradient K for the potentiometer is given by:
K=EL
where E is the electromotive force (emf) and L is the length of the wire.
V1=K⋅L1
V2=K⋅L2
K⋅L1=I1⋅(R1+r)
K⋅L2=I2⋅(R2+r)
The current I through the circuit can be expressed using Ohm's law:
I=ER+r
Thus, we can express I1 and I2 as:
I1=ER1+r
I2=ER2+r
Substituting I1 and I2 into the equations gives:
K⋅L1=ER1+r⋅(R1+r)
K⋅L2=ER2+r⋅(R2+r)
From the two equations, we can set up a ratio:
L1L2=R1+rR2+r
Substituting the known values:
32=8+r4+r
Cross-multiplying gives:
3(4+r)=2(8+r)
Expanding both sides:
12+3r=16+2r
Rearranging gives:
3r−2r=16−12
r=4Ω
The internal resistance r is 4Ω.
Topper's Solved these Questions
Similar Questions
A potentiometer circuit with potentiometer wire 10 m long, and an ideal main battery of e.m.f 8 V, has been set up for finding the internal resistance of a given cell. When the resistance R, connected across the given cell, has values of (i) infinity, (ii) 10 omega , the balancing lengths, on the potentiometer wire are found to be 2.4 m and x respectively. If the internal resistance of the cell is 2 omega, the value of x is
View SolutionIn an experiment with potentiometer to measure the internal resistance of a cell when the cell is shunted by 5Ω the null point is obtained at 2m .When the cell is shunted by 10Ω the null point is obtained at 3m .The internal resistance of the cell is
View Solution
Knowledge Check
The e.m.f. of a standard cell balances across 150 cm length of a wire of potentiometer. When a resistance of 2Ω is connected as a shunt with the cell, the balance point is obtained at 100cm . The internal resistance of the cell is
A0.1ohmB1ohmC2ohmD0.5ohmFigure shows the circuit of a potentiometer . The length of the potentiometer wire AB is 50 cm . The e.m.f of the battery E1 is 4 volt , having negligible internal resistance . Values of resistance R1andR2 are 15 ohm and 5 ohm respectively . When both the keys are open, the null point is obtained at a distance of 31.25 cm from end A but when both the keys are closed , the balance length reduce to 5 cm only. Given RAB=10Ω
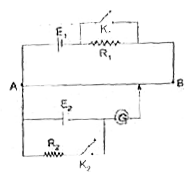
The internal resistance of the cell E2 isA4.5ΩB5.5ΩC6.5ΩD7.5ΩFigure shows the circuit of a potentiometer . The length of the potentiometer wire AB is 50 cm . The e.m.f of the battery E1 is 4 volt , having negligible internal resistance . Values of resistance R1andR2 are 15 ohm and 5 ohm respectively . When both the keys are open, the null point is obtained at a distance of 31.25 cm from end A but when both the keys are closed , the balance length reduce to 5 cm only. Given RAB=10Ω
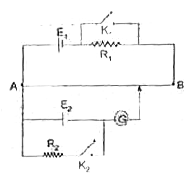
The e.m.f of the cell E2 isA1 voltB2 voltC3 voltD4 volt
Find power in entire circuit where internal resistance is 0.6 ohm.
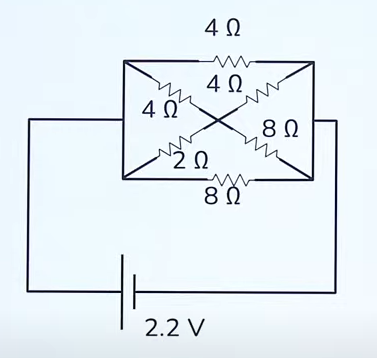
View SolutionA potentiometer circuit has been set up for finding the internal resistance of a given cell. The main battery, used across the potentiometer wire , has an emf of 2.0 v and a negligible internal resistance .The potentiometer wire itself is 4 m long . When the resistance , R connected across the given cell, has values of (i) Infinity , (ii) 9.5Ω the balancing length's on the potentiometer wire are found to be 3 m and 2.85 m , respectively . The value of internal resistance of the cell is .
View SolutionIn the given potentiometer circuit length of the wire AB is 3m and resistance is R=4.5Ω. The length AC for no deflection in galvanometer is
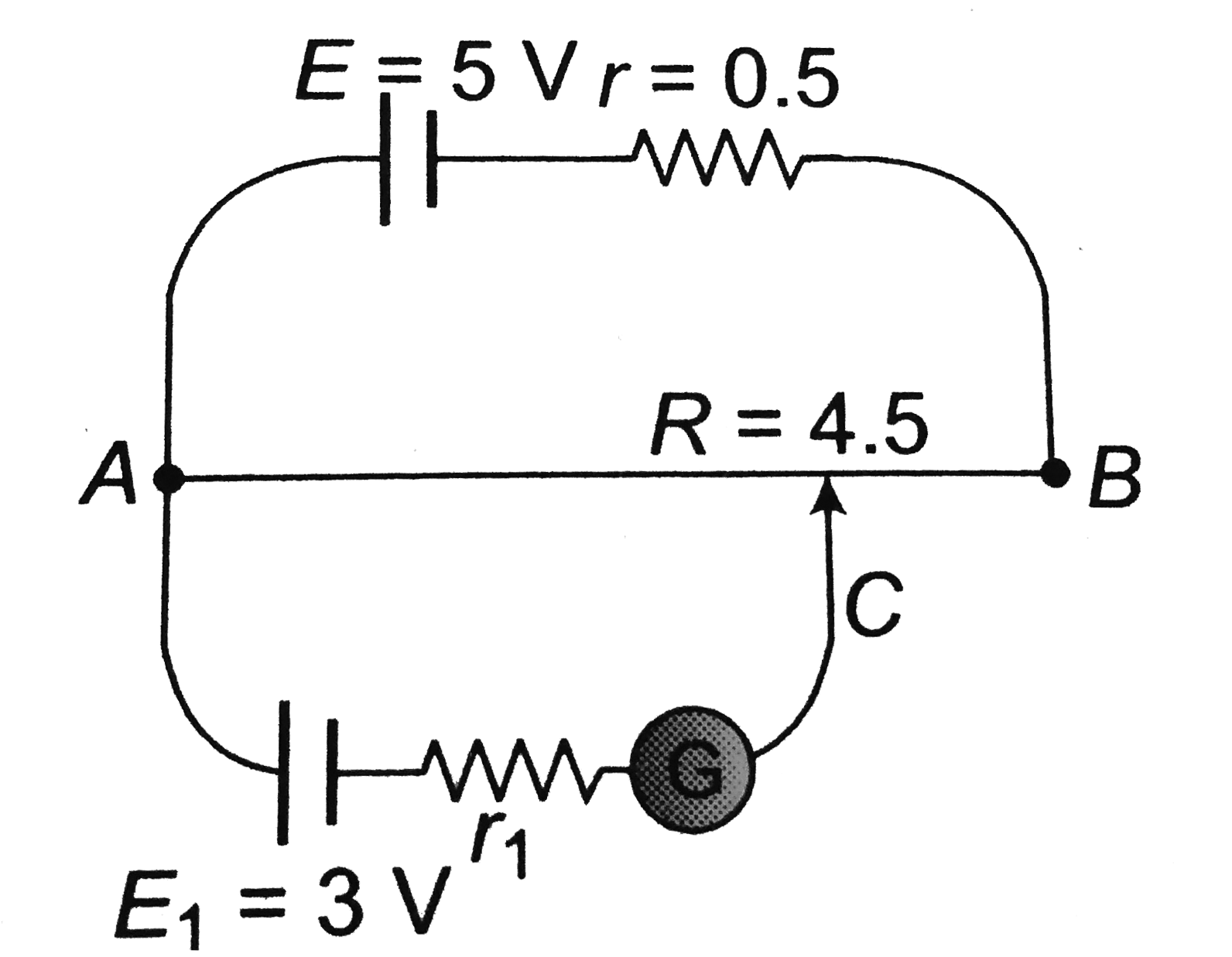
View SolutionA potentiometer circuit has been setup for finding. The internal resistance of a given cell. The main battery used a negligible internal resistance. The potentiometer wire itself is 4m long. When the resistance, R, connected across the given cell, has value of
(i) Infinity 9.5Ω,
(ii) the 'balancing length' , on the potentiometer wire are found to be 3m and 2.85m, respectively.
The value of internal resistance of the cell is
View SolutionIn an experiment of meter bridge, a null point is obtaining at the center of the bridge wire. When a resistance of 10ohm is connected in one gap, the value of resistance other gap is
View Solution
