A bar of length l carrying a small mass m at one of its ends rotates with a uniform angular speed ω in a vertical plane about the mid-point of the bar . During the rotation, at some instant of time when the bar is horizontal, the mass is detached from the bar but the bar continues to rotate with same ω . The mass moves vertically up, comes back and reaches the bar at the same point. At that place, the acceleration due to gravity is g
This is possible if the quantity ω2l2πg is an integer
The total time of flight of the mass is proportional to ω2
The total distance travelled by the mass in air is proportional to ω2
The total distance travelled by the mass in air and its total time of flight are both independent on its mass
The correct Answer is:A, C, D
Velocity
v=l2ω
T=2vg=lωg

Let no. of rotation = n (within T times)
nT=Iωg
⇒n.2πω=lωg⇒n=lω22πg
Similar Questions
लम्बाई की एक छड़, जिसके एक सिरे पर कम द्रव्यमान m लटका हुआ है छड़ के मध्य बिन्दु के लगभग ऊर्ध्वाधर समतल में एक समान कोणीय गति ωसे घूर्णन कर रही है। घूर्णन के दौरान, किसी समय जब छड़ क्षैतिज हो जाती है तो भार छड़ से अलग हो जाता है परंतु छड तब भी समान कोणीय गति ω से लगातार घूर्णन करती रहती है। भार ऊर्ध्वाधर ऊपर की ओर गति करके छड़ के उसी बिन्दु पर वापस आ जाता है। उस स्थान पर गुरुत्व के दौरान त्वरण होगा।
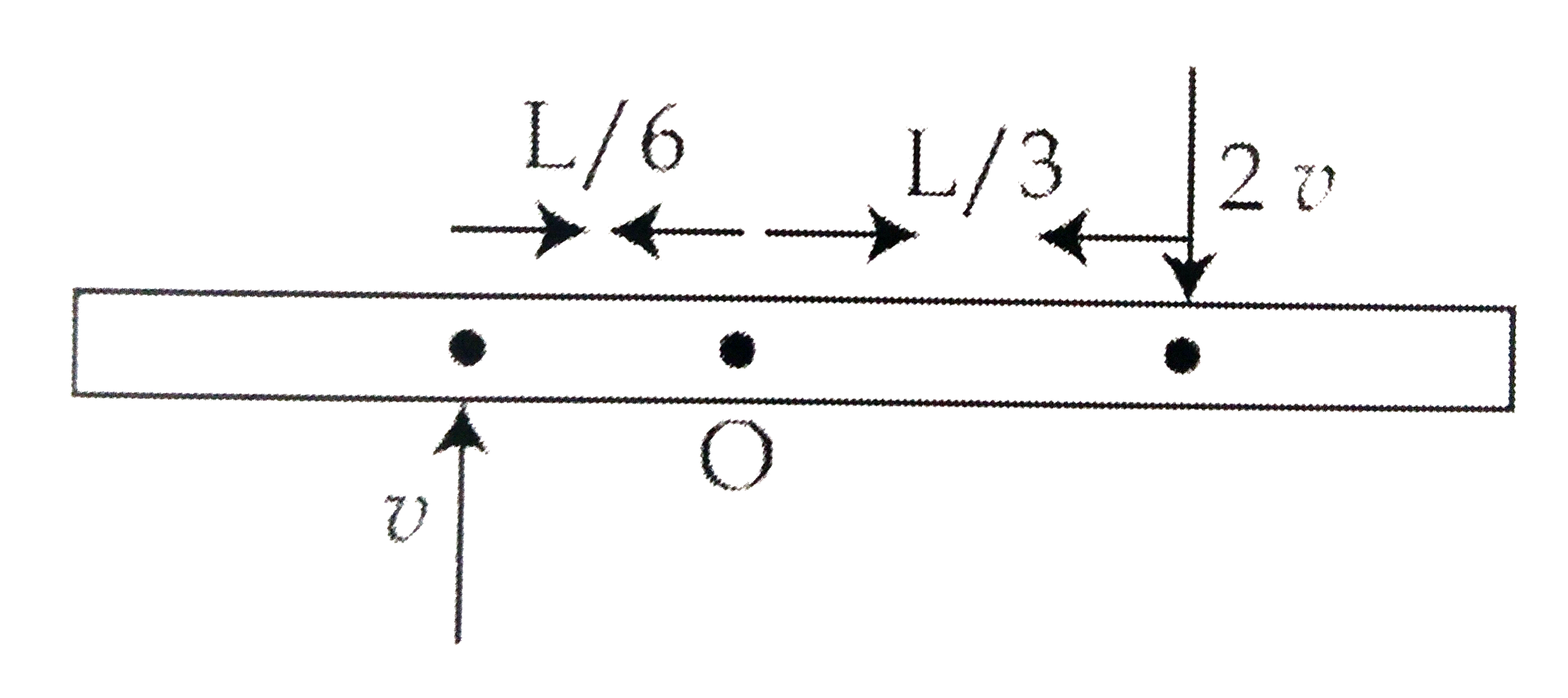
View SolutionA thin uniform bar of length L and mass 8m lies on a smooth horizontal table .Two point masses m and 2 m are moving in the same horizontal plane from opposite sides of the bar with speeds 2v and v respectively .The masses stick to the bar after collision at a distances L3andL6 respectively from the center of the bar if the bar starts rotating about its center of mass as result of collision the angular speed of the bar will be
View SolutionA bar of length l canying a small mass m at one of its ends rotates with a uniform angular speed omega in a vertical plane about the mid-point of the bar. During the rotation, at some instant of time when the bar is horizontal, the mass is detached from the bar but the bar continues to rotate with same omega . The mass moves ve1tically up, comes back and reaches the bar at the same point. At that place, the acceleration due to gravity is g.
View SolutionA bar of length l carrying a small mass m at one of its ends rotates with a uniform angular speed ω in a vertical plane about the mid-point of the bar. During the rotation, at some instant of time when the bar is horizontal, the mass is detached from the bar but the bar continues to rotate with same ω. The mass moves vertically up, comes back and reaches the bar at the same point. At that place, the acceleration due to gravity is g.
View SolutionA uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity omega about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
View SolutionA bar of length l carrying a small mass m at one of its ends rotates with a uniform angular speed omega in a vertical plane about the midpoint of the bar. During the rotation, at some instant of time with the bar is horizontal, the mass Is detached from the bar but the bar continues to rotate with same omega . The mass moves vertically up, comes back and reaches the bar at the same point. At that place, the acceleration due to gravity is g.
View SolutionA bar of length l carrying a small mass m at one of its ends rotates with a uniform angular speed ω in a vertical plane about the midpoint of the bar. During the rotation, at some instant of time with the bar is horizontal, the mass is detached from the bar but the bar continues to rotate with same ω. The mass moves vertically up, comes back and reaches the bar at the same point. At that place, the acceleration due to gravity is g
View SolutionA rod AB of mass m and length L is rotating in horizontal plane about one of its ends which is pivoted. The constant angular speed with which the rod is rotating is omega . The force applied on the rod by the pivot is
View Solution
