A uniform thin rod AB of mass M and length l attached to a string OA of length $\frac{l}{2}$ is placed on a smooth horizontal plane and rotates with angular velocity omega around a vertical axis through O. A peg P is inserted in the plane in order that on striking it the bar will come exactly to rest

Location of peg for rod coming to rest is $r = \frac{5 l}{6}$

Location of peg for rod coming to rest is $r = \frac{3 l}{4}$

Location of peg for rod coming to rest is $r = \frac{13}{12}$

Location of peg for rod coming to rest is $r = \frac{2 l}{3}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Updated on:21/07/2023

A uniform thin rod AB of mass M and length l attached to a string OA of length $= \frac{1}{2}$ is supported by a smooth horizontal plane and rotates with angular velocity $ω$ around a vertical axis through O. A peg P is inserted in the plane in order that on striking it the rod will come to rest.

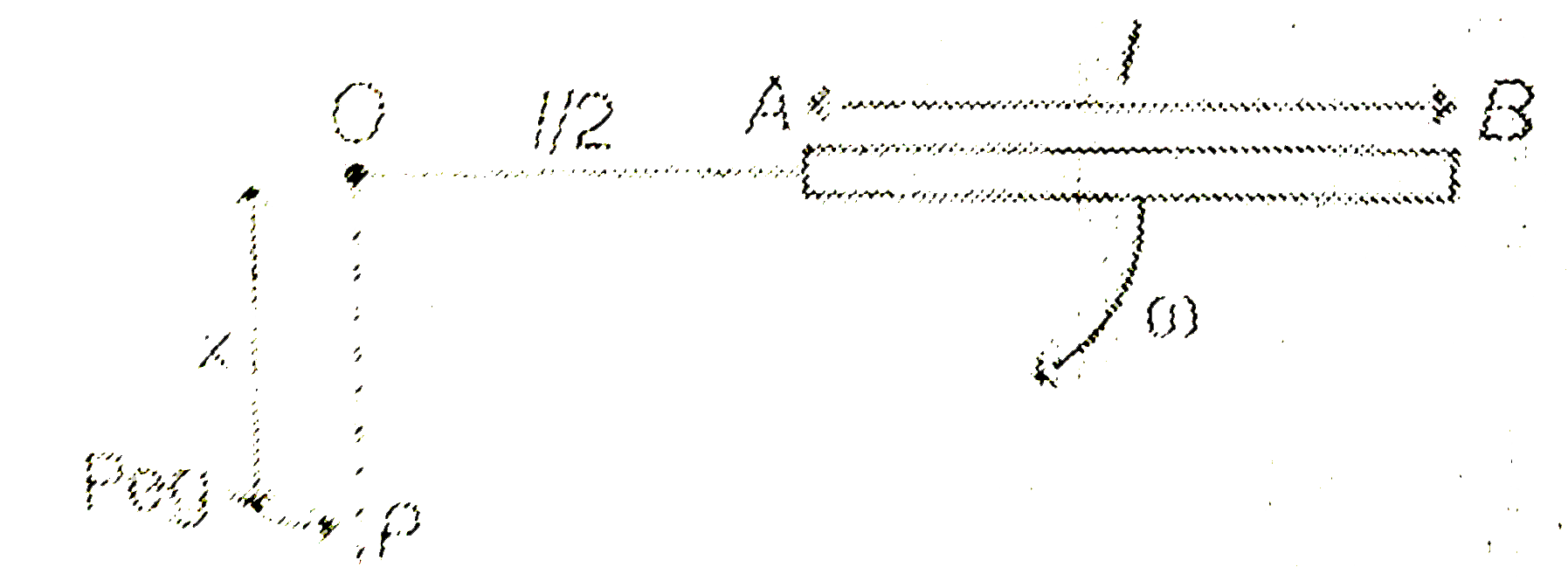Amagnitude of angular momentum of rod about O is $\frac{4}{3} l^{2} ω$
BMagnitude of tension in string is $M / ω^{2}$
CLocation of peg for rod coming to rest is x $= \frac{13}{12} l$
Dmagnitude of angular impulse by peg on the rod is $\frac{4}{3} l^{2} ω$
A uniform rod of mass $m$ and length $l$ rotates in a horizontal plane with an angular velocity $ω$ about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
A $\frac{1}{2} m ω^{2} x$
B $\frac{1}{2} m ω^{2} (1 - \frac{x^{2}}{l})$
C $\frac{1}{2} m ω^{2} l (1 - \frac{x^{2}}{l^{2}})$
D $\frac{1}{2} m ω^{2} l [1 - \frac{x}{l}]$
A uniform stick of length l and mass m lies on a smooth table. It rotates with angular velocity $ω$ about an axis perpendicular to the table and through one end of the stick. The angular momentum of the stick about the end is
A $m l^{2} ω$
B $\frac{m l^{2} ω}{3}$
C $\frac{m l^{2} ω}{12}$
D $\frac{m l^{2} ω}{6}$