A fighter jet is flying, horizontally at a certain altitude with a speed of 200 ms−1. When it passes directly overhead an anti-aircraft gun, a bullet is fired from the gun, at an angle θ with the horizontal, to hit the jet. If the bullet speed is 400 m/s, the value of θ will be _______.
To solve the problem, we need to determine the angle θ at which the bullet must be fired from the anti-aircraft gun to hit the fighter jet flying horizontally at a speed of 200 m/s. The bullet is fired at a speed of 400 m/s at an angle θ with respect to the horizontal.
1. Identify the horizontal component of the bullet's velocity:
The horizontal component of the bullet's velocity can be expressed as:
vbx=vbcos(θ)
where vb=400m/s is the speed of the bullet.
2. Set the horizontal components equal:
For the bullet to hit the jet, the horizontal component of the bullet's velocity must equal the horizontal speed of the jet:
vbx=vj
where vj=200m/s is the speed of the jet.
Therefore, we have:
400cos(θ)=200
3. Solve for cos(θ):
Rearranging the equation gives:
cos(θ)=200400=12
4. Find θ:
To find θ, we take the inverse cosine:
θ=cos−1(12)
The angle whose cosine is 12 is:
θ=60∘orπ3 radians
Final Answer:
Thus, the value of θ is:
θ=π3 radians
The horizontal component of the bullet's velocity can be expressed as:
vbx=vbcos(θ)
where vb=400m/s is the speed of the bullet.
For the bullet to hit the jet, the horizontal component of the bullet's velocity must equal the horizontal speed of the jet:
vbx=vj
where vj=200m/s is the speed of the jet.
400cos(θ)=200
Rearranging the equation gives:
cos(θ)=200400=12
To find θ, we take the inverse cosine:
θ=cos−1(12)
The angle whose cosine is 12 is:
θ=60∘orπ3 radians
Thus, the value of θ is:
θ=π3 radians
Topper's Solved these Questions
- JEE MAINS 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - PHYSICS (SECTION A)
20 Videos
- JEE MAINS 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - PHYSICS (SECTION B)
10 Videos
- JEE MAINS 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - PHYSICS- SECTION A (ASSERTION (A) REASON (R))
1 Videos
- JEE MAINS 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2021EXERCISE - Physics (Section B )
10 Videos
- JEE MAINS 2023 JAN ACTUAL PAPERBOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2023 JAN ACTUAL PAPEREXERCISE - Question
360 Videos
Similar Questions
A fighter plane flying horizontally at an altitude of 1.5km with speed of 720kmh9−10 passes directlu overhead an anticraft gun. At what anle fro the gun with muzzle speed 400ms−1 to hit the plane in shortest time ?
View SolutionA fighter plane flying horizontally at an altitude of 2km with speed of 540 kmph passes directly over head an anti aircraft gun.If the gun can fire a bullet at the muzzle speed of 500ms−1,at what angle with the vertical the gun should fire the bullet so that the bullet hits the plane?
View Solution
Knowledge Check
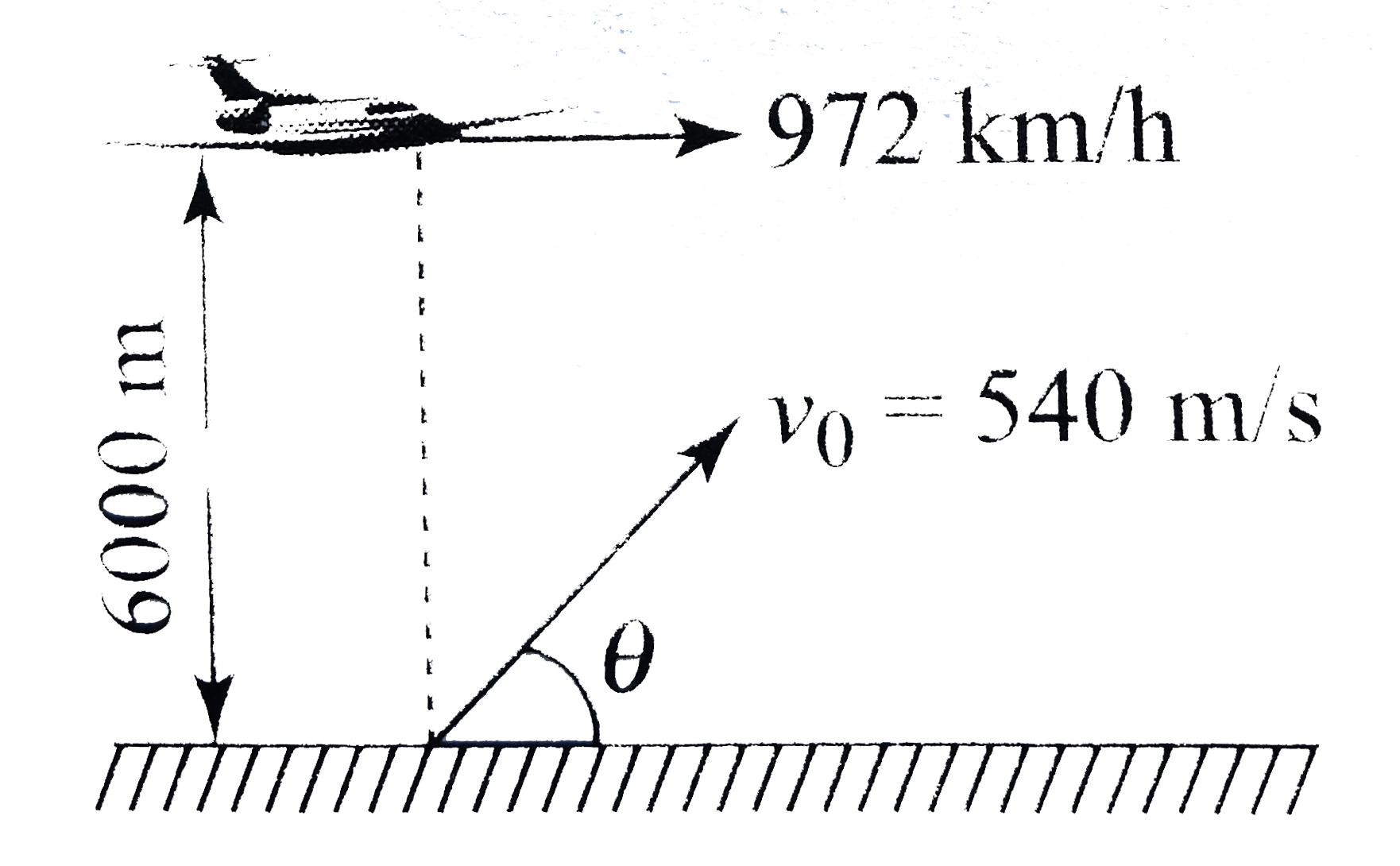
An aircraft moving with a speed of 1000 km/h is at a heirgh of 6000 m, just overhead of an anti-aircraft gun. If the muzzle velocity of the gun is 540 m/s, the firing angle θ for the bullet to hit the aircraft should beA73∘B30∘C60∘D45∘An aircraft moving with a speed of 250m/s is at a height of 6000m,just overhead of an antiaircraft gun.If the muzzle velocity is 500m/s,the firing angle θ should be:
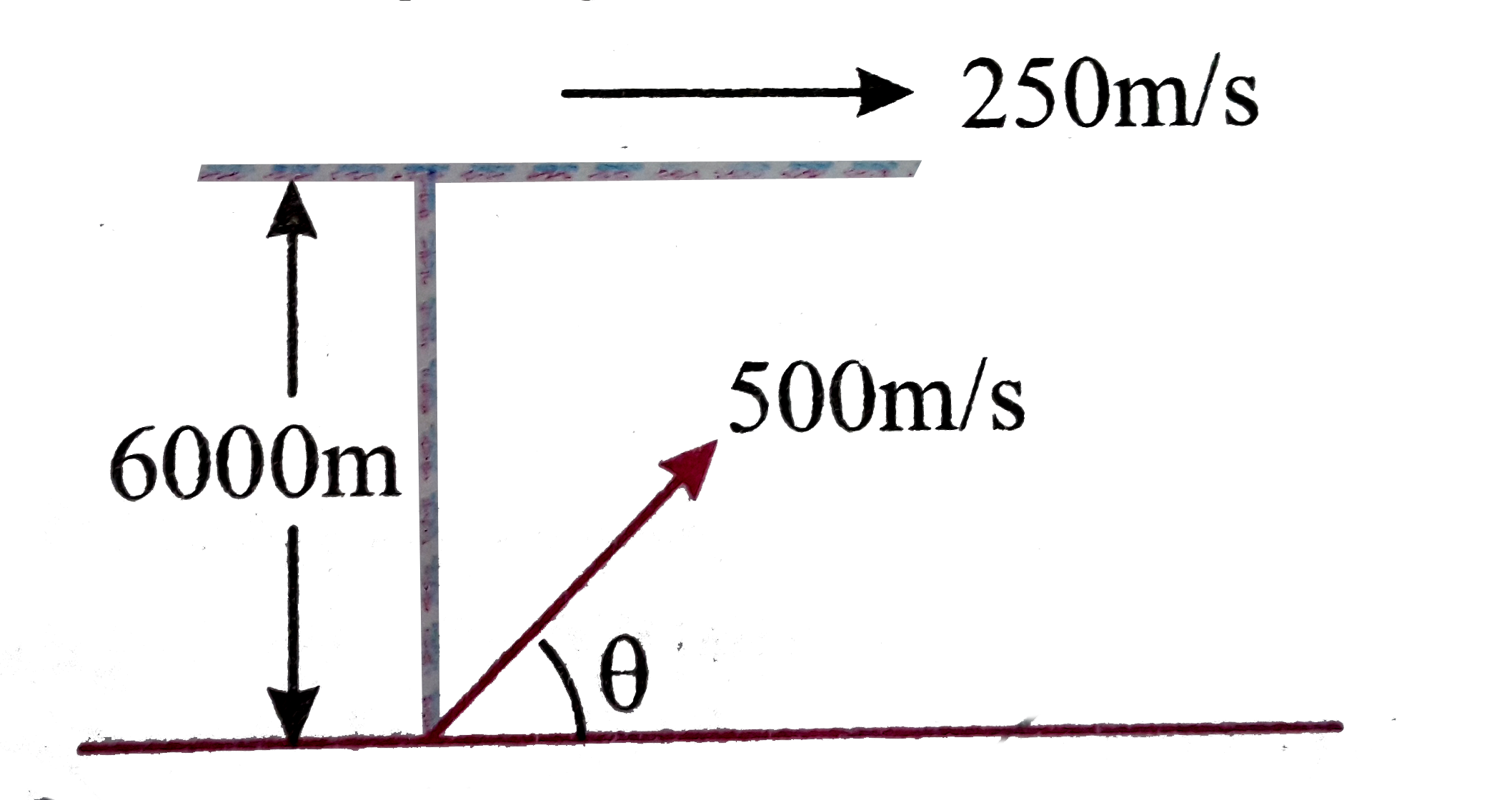 A30∘B45∘C60∘Dnone of these
A30∘B45∘C60∘Dnone of these
A fightre plane flying horizontally at an altitude oa 1.5km with speed 720h−1 passes directly over head an anticraft gun. At what angle from the vertical should the gun be fired from the shell with muzzle speed 600ms−1 to hit plane. At what minimum altitude showld the pilot fly the plane to avoid being hit ? ( Take g= 10 ms^(-2)).
View SolutionAn enemy plane is flying horizontally at an altitude of 2km with a speed of 300ms−1.An army man with an anti-aircraft gun on the ground sights enemy plane when it is directly overhead and fires a shell with a muzzle speed of 600ms−1.At what angle with the vertical should the gun be fired so as to hit the plane?
View SolutionAn enemy air plane is flying horizontally at an altitude of 2.7km with a speed of 250ms−1 .An army man on the ground observed it when it is directly over his head.He fired an anti-aircraft gun with a muzzle speed of 500ms−1 ,such that the shell hits the plane.At what angle with the horizontal,gun should be fired?
View SolutionA 50 g bullet is fired from a 10 kg gun with a speed of 500 ms−1. What is the speed of the recoil of the gun.
View SolutionAn aircraft moving with a speed of 250 m/s is at a height of 6000 m, just overhead of an anti aircraft–gun. If the muzzle velocity is 500 m/s the firing angle θ should be:
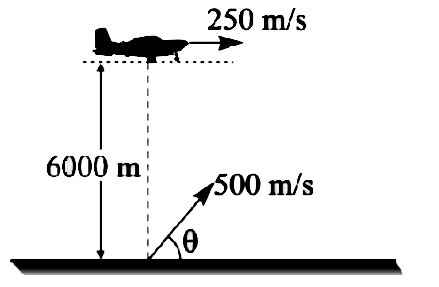
View SolutionA bullet is fired with speed 50m/s at 45∘ angle with horizontal. Find the height of the bullet when its direction of motion makes angle 30∘ with the horizontal.
View Solution
