In the $Δ A B C$ (sec figure ) $∠ A$ = right angle $A B = \sqrt{x} and B C = \sqrt{x + 5}$ . Evaluate

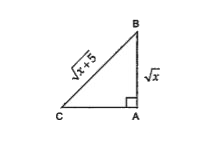
$sin C . cos tan C + {cos}^{2} C . sin A$

Text Solution

Verified by Experts

The correct Answer is:1

Updated on:21/07/2023

|

Class 10 MATHS TRIGONOMETRIC RATIOS AND IDENTITIES

Topper's Solved these Questions

INTRODUCTION TO TRIGONOMETRY BOOK - OSWAL PUBLICATIONCHAPTER - INTRODUCTION TO TRIGONOMETRY EXERCISE - Assertion and Reasoning Based Questions
5 Videos
INTRODUCTION TO TRIGONOMETRY BOOK - OSWAL PUBLICATIONCHAPTER - INTRODUCTION TO TRIGONOMETRY EXERCISE - Case Based Questions
15 Videos
INTRODUCTION TO TRIGONOMETRY BOOK - OSWAL PUBLICATIONCHAPTER - INTRODUCTION TO TRIGONOMETRY EXERCISE - Short Answer Type Questions
22 Videos
DIKSHA QUESTIONS BOOK - OSWAL PUBLICATIONCHAPTER - DIKSHA QUESTIONS EXERCISE - UNIT -VII: Statistics and Probability (Probability) (Long Answer Type Questions )
12 Videos
INTRODUCTION TO TRIGONOMETRY AND TRIGONOMETRIC IDENTITIES BOOK - OSWAL PUBLICATIONCHAPTER - INTRODUCTION TO TRIGONOMETRY AND TRIGONOMETRIC IDENTITIES EXERCISE - BOARD CORNER (Long Solution Type Questions)
6 Videos

Similar Questions

Knowledge Check

In a $Δ A B C$ right angled at B, if tan $A = \frac{1}{\sqrt{3}}$ , find the value of cos A cos C - sin A sin C
A1
B0
C $- 1$
D2

OSWAL PUBLICATION-INTRODUCTION TO TRIGONOMETRY -Long Answer Type Questions

Home
Ask Doubt
Profile