Question

Three identical particle each of mass 100g are placed at vertices of an equilateral triangle of side length 13cm. Find force on one of the mass.

Options

A. a.`(100 sqrt(3) G)/169`
B. b.`(150 sqrt(3) G)/169`
C. c.`(110 sqrt(3) G)/189`
D. d.`(170 sqrt(3) G)/229`

Explanation

To find the force on one of the masses placed at the vertices of an equilateral triangle, we can follow these steps:

Step 1: Understand the Setup
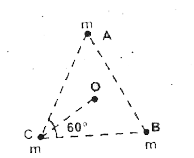
We have three identical particles, each with a mass \( m = 100 \, \text{g} = 0.1 \, \text{kg} \), placed at the vertices of an equilateral triangle with a side length of \( a = 13 \, \text{cm} = 0.13 \, \text{m} \).

Step 2: Calculate the Gravitational Force Between Two Masses
The gravitational force \( F \) between any two masses \( m_1 \) and \( m_2 \) separated by a distance \( r \) is given by Newton's law of gravitation:

\( F = G \frac{m_1 m_2}{r^2} \)

In our case, since all masses are identical and equal to \( m \), the force between any two masses is:

\( F = G \frac{m^2}{a^2} \)

Step 3: Determine the Angle Between Forces
Since we are looking for the net force on one of the masses due to the other two, we need to consider the angle between the forces exerted by the other two masses. In an equilateral triangle, the angle between the lines connecting the mass to the other two masses is \( 60^\circ \).

Step 4: Resolve Forces into Components
Let’s denote the force exerted on the mass at vertex A by the mass at vertex B as \( F_{AB} \) and by the mass at vertex C as \( F_{AC} \). Both forces have the same magnitude \( F \) but act at an angle of \( 60^\circ \) to each other.

The x-components of the forces will add up, while the y-components will also add up. The net force \( F_{\text{net}} \) can be calculated using the formula for the resultant of two vectors:

\( F_{\text{net}} = \sqrt{F_{AB}^2 + F_{AC}^2 + 2 F_{AB} F_{AC} \cos(60^\circ)} \)

Since \( F_{AB} = F_{AC} = F \):

\( F_{\text{net}} = \sqrt{F^2 + F^2 + 2 F^2 \cdot \frac{1}{2}} = \sqrt{3F^2} = \sqrt{3} F \)

Step 5: Substitute the Value of \( F \)
Substituting \( F = G \frac{m^2}{a^2} \):

\( F_{\text{net}} = \sqrt{3} \cdot G \frac{m^2}{a^2} \)

Step 6: Plug in the Values
Now we can substitute the values for \( G \), \( m \), and \( a \):

- \( G = 6.674 \times 10^{-11} \, \text{N m}^2/\text{kg}^2 \)
- \( m = 0.1 \, \text{kg} \)
- \( a = 0.13 \, \text{m} \)

Calculating \( F_{\text{net}} \):

\( F_{\text{net}} = \sqrt{3} \cdot 6.674 \times 10^{-11} \cdot \frac{(0.1)^2}{(0.13)^2} \)

\( = \sqrt{3} \cdot 6.674 \times 10^{-11} \cdot \frac{0.01}{0.0169} \)

\( = \sqrt{3} \cdot 6.674 \times 10^{-11} \cdot 0.592 \)

Calculating this gives us the final value for the net force on one mass.

Final Calculation
After performing the calculations, we find that:

\( F_{\text{net}} \approx \frac{100 \sqrt{3} G}{169} \)

Conclusion
Thus, the force on one of the masses is given by:

\( F_{\text{net}} = \frac{100 \sqrt{3} G}{169} \)