A capacitor is being charged from 0 to a maximum of Voltage across the capacitor varies as
To solve the problem, we need to determine how the voltage across a capacitor varies as it is charged from 0 to a maximum charge of 5 µC. We will use the relationship between charge (Q), capacitance (C), and voltage (V) given by the formula:
Q=C⋅V
1. Identify the given values:
- Capacitance, C=2μF=2×10−6F
- Maximum charge, Qmax=5μC=5×10−6C
2. Use the formula to find the voltage:
- Rearranging the formula Q=C⋅V gives us:
V=QC
3. Calculate the voltage when the charge is at its maximum:
- Substitute Qmax and C into the equation:
Vmax=5×10−6C2×10−6F=52V=2.5V
4. Analyze the relationship between charge and voltage:
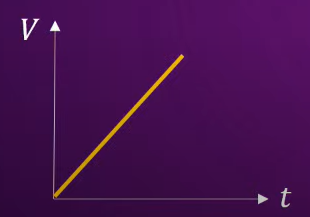
- Since capacitance C is constant, the voltage V is directly proportional to the charge Q. As the charge increases from 0 to Qmax, the voltage will increase linearly from 0 to Vmax.
5. Graphical representation:
- The graph of voltage V versus charge Q will be a straight line starting from the origin (0,0) and reaching the point (5 µC, 2.5 V).
6. Conclusion:
- The voltage across the capacitor varies linearly with the charge. Therefore, the correct representation of this relationship is a straight line graph.
Final Answer:
The voltage across the capacitor varies linearly as it is charged from 0 to 5 µC, reaching a maximum of 2.5 V.
- Capacitance, C=2μF=2×10−6F
- Maximum charge, Qmax=5μC=5×10−6C
- Rearranging the formula Q=C⋅V gives us:
V=QC
- Substitute Qmax and C into the equation:
Vmax=5×10−6C2×10−6F=52V=2.5V
- Since capacitance C is constant, the voltage V is directly proportional to the charge Q. As the charge increases from 0 to Qmax, the voltage will increase linearly from 0 to Vmax.
- The graph of voltage V versus charge Q will be a straight line starting from the origin (0,0) and reaching the point (5 µC, 2.5 V).
- The voltage across the capacitor varies linearly with the charge. Therefore, the correct representation of this relationship is a straight line graph.
The voltage across the capacitor varies linearly as it is charged from 0 to 5 µC, reaching a maximum of 2.5 V.
Topper's Solved these Questions
Similar Questions
A 10μF capacitor can withstand a maximum voltage of 100 V across it,whereas another 20μF capacitor can withstand a maximum voltage of only 25 V. What is the maximum voltage that can be put across their series combination ?
View SolutionA capacitor charged to 10 V is being discharged through a resistance R. At the end of 1 s, the voltage across the capacitor is 5V. What will be the voltage after 2 s?
View Solution
Knowledge Check
The 500μF capacitor is charged at a steady rate of 100μC/s. The potential difference across the capacitor will be 10 V after an interval of
A80secB50secC20secD40secLet q be the charge on the capacitor at any time t. The voltage V across the capacitor is
AVmsinωt=qCBVmcosωt=2VCCVmcosωt=q2CDVmsinωt=2qC
In the figure an A.C of rms voltage 200 volt is appled to the circuit containing diode and the capacitor and it is being rectified. The maximum potential across the capacitor C in volt will beA500B200C283D141
A 10μF capacitor is charged to a potential of 25 V. The battery is then disconnected and a pure 100 mH coil is connected across the capacitor so that LC oscillations are set-up. What is the maximum current in the coil ?
View SolutionA varying voltage is applied to the clamps AB as shown in fig. such that the voltage across the capacitor plates varies as shown in the figure. Plot the time depending on voltage across the clapes CD.
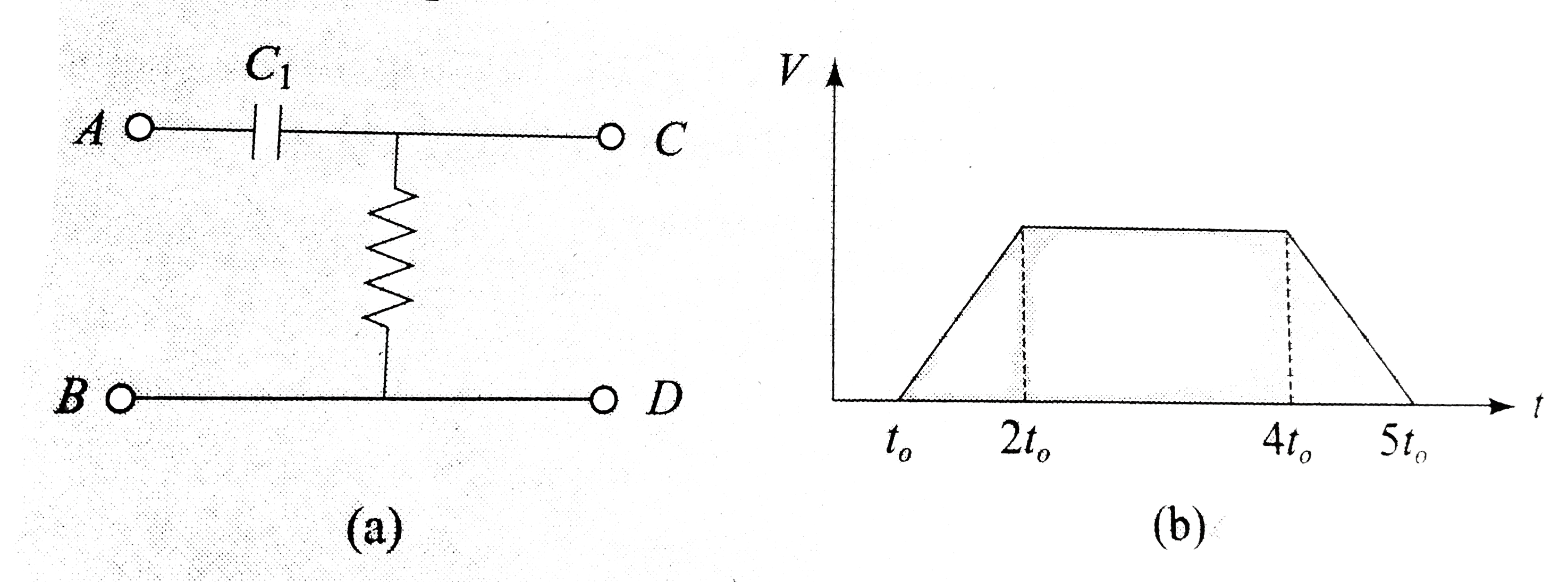

View SolutionAn oscillator circuit contains an inductor 0.05 H and a capacitor of capacity 80μF. When the maximum voltage across the capacitor is 200 V, the maximum current (in amperes) in the circuit is
View SolutionA 2μF capacitor is charged with 10 volt cell. Now cell is removed and this capacitor is connected with uncharged 8μF capacitor. Find out final charge on 8μF capacitor.
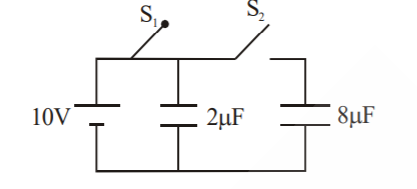
View SolutionA 100μF capacitor is charged with a 50 V source supply. Then source supply is removed and the capacitor is connected across an inductor, as a result of which 5 A current flows through the inductance. Calculate the value of inductance.
View Solution
