A solid spherical ball is half submerged in liquid is at equilibrium. Density ball is ρkgm3 density of liquid is σkgm3 and surface tension of liquid is T. Find radius of ball.
To solve the problem of finding the radius of a solid spherical ball that is half submerged in a liquid at equilibrium, we can follow these steps:
1. Understanding the Forces Acting on the Ball:
- The ball experiences three main forces:
- The weight of the ball (W_ball).
- The buoyant force (F_buoyancy) acting upwards.
- The surface tension force (F_surface_tension) acting along the surface of the liquid.
2. Calculating the Weight of the Ball:
- The weight of the ball can be expressed as:
Wball=ρ⋅Vball⋅g
- The volume Vball of a sphere is given by 43πR3, so:
Wball=ρ⋅(43πR3)⋅g
3. Calculating the Buoyant Force:
- The buoyant force is equal to the weight of the liquid displaced by the submerged part of the ball:
Fbuoyancy=σ⋅Vdisplaced⋅g
- Since the ball is half submerged, the volume of the displaced liquid is 12Vball:
Fbuoyancy=σ⋅(12⋅43πR3)⋅g=23σπR3g
4. Calculating the Surface Tension Force:
- The surface tension force acts along the circumference of the submerged part of the ball:
Fsurface tension=T⋅2πR
5. Setting Up the Equilibrium Condition:
- For the ball to be in equilibrium, the sum of the upward forces (buoyant force + surface tension force) must equal the downward force (weight of the ball):
Fbuoyancy+Fsurface tension=Wball
- Substituting the expressions we found:
23σπR3g+T⋅2πR=ρ⋅(43πR3)g
6. Simplifying the Equation:
- Cancel out π from both sides:
23σR3g+2TR=43ρR3g
- Rearranging gives:
43ρR3g−23σR3g=2TR
- Factoring out R3g:
R3g(43ρ−23σ)=2TR
7. Solving for Radius R:
- Dividing both sides by R (assuming R≠0):
R2g(43ρ−23σ)=2T
- Rearranging gives:
R2=2Tg(43ρ−23σ)
- Taking the square root:
R=
⎷2Tg(43ρ−23σ)
Final Result:
The radius R of the ball is given by:
R=
⎷2Tg(43ρ−23σ)
- The ball experiences three main forces:
- The weight of the ball (W_ball).
- The buoyant force (F_buoyancy) acting upwards.
- The surface tension force (F_surface_tension) acting along the surface of the liquid.
- The weight of the ball can be expressed as:
Wball=ρ⋅Vball⋅g
- The volume Vball of a sphere is given by 43πR3, so:
Wball=ρ⋅(43πR3)⋅g
- The buoyant force is equal to the weight of the liquid displaced by the submerged part of the ball:
Fbuoyancy=σ⋅Vdisplaced⋅g
- Since the ball is half submerged, the volume of the displaced liquid is 12Vball:
Fbuoyancy=σ⋅(12⋅43πR3)⋅g=23σπR3g
- The surface tension force acts along the circumference of the submerged part of the ball:
Fsurface tension=T⋅2πR
- For the ball to be in equilibrium, the sum of the upward forces (buoyant force + surface tension force) must equal the downward force (weight of the ball):
Fbuoyancy+Fsurface tension=Wball
- Substituting the expressions we found:
23σπR3g+T⋅2πR=ρ⋅(43πR3)g
- Cancel out π from both sides:
23σR3g+2TR=43ρR3g
- Rearranging gives:
43ρR3g−23σR3g=2TR
- Factoring out R3g:
R3g(43ρ−23σ)=2TR
- Dividing both sides by R (assuming R≠0):
R2g(43ρ−23σ)=2T
- Rearranging gives:
R2=2Tg(43ρ−23σ)
- Taking the square root:
R=
⎷2Tg(43ρ−23σ)
The radius R of the ball is given by:
R=
⎷2Tg(43ρ−23σ)
Topper's Solved these Questions
Similar Questions
Two identical balls each having a density ρ are suspended from as common point by two insulating strings of equal length. Both the balls have equal mass and charge. In equilibrium each string makes an angle θ with vertical. Now, both the balls are immersed in a liquid. As a result the angle θ does not change. The density of the liquid is σ. Find the dielectric constant of the liquid.
View SolutionA ball weighs 80 g in air 60g in water and 50g in liquid if the density of water is 1gcm−3 find the density of this liquid.
View Solution
Knowledge Check
A sphere of density ρ is half submerged in a liquid of density σ and surface tension T. The sphere remains in equilibrium. Find radius of the sphere (assume the force due to surface tension acts tangentially to surface of sphere)
A√T(ρ−σ)gB√T(ρ−2σ)gC√2T(2ρ−3σ)gD√3T(2ρ−σ)gA capillary of radius 0.15mm is dipped in liquid of density 'rho' = 667 kg/m^3. If surface tension of liquid is 120Nm then find height upto which liquid rises in capillary. Angle of contact between liquid and capillary tube is 60∘. (g=10ms2)
A0.01mB0.02mC0.04mD0.05mA needle of length l and density ρ will float on a liquid of surface tension σ if its radius r is less than or equal to:
A√2σπρlgB√2σlπρgC√σπρgD√2σπρg
A wood is of density 680kg/m3. It is submerged in three liquids. Those are alcohol, water and glycerine. The density of alcohol is 780kg/m3. The density of waer is 1g/cm3 and the density of glycerine is 1.250g/cm3. In which liquid is the wood less submerged?
View Solution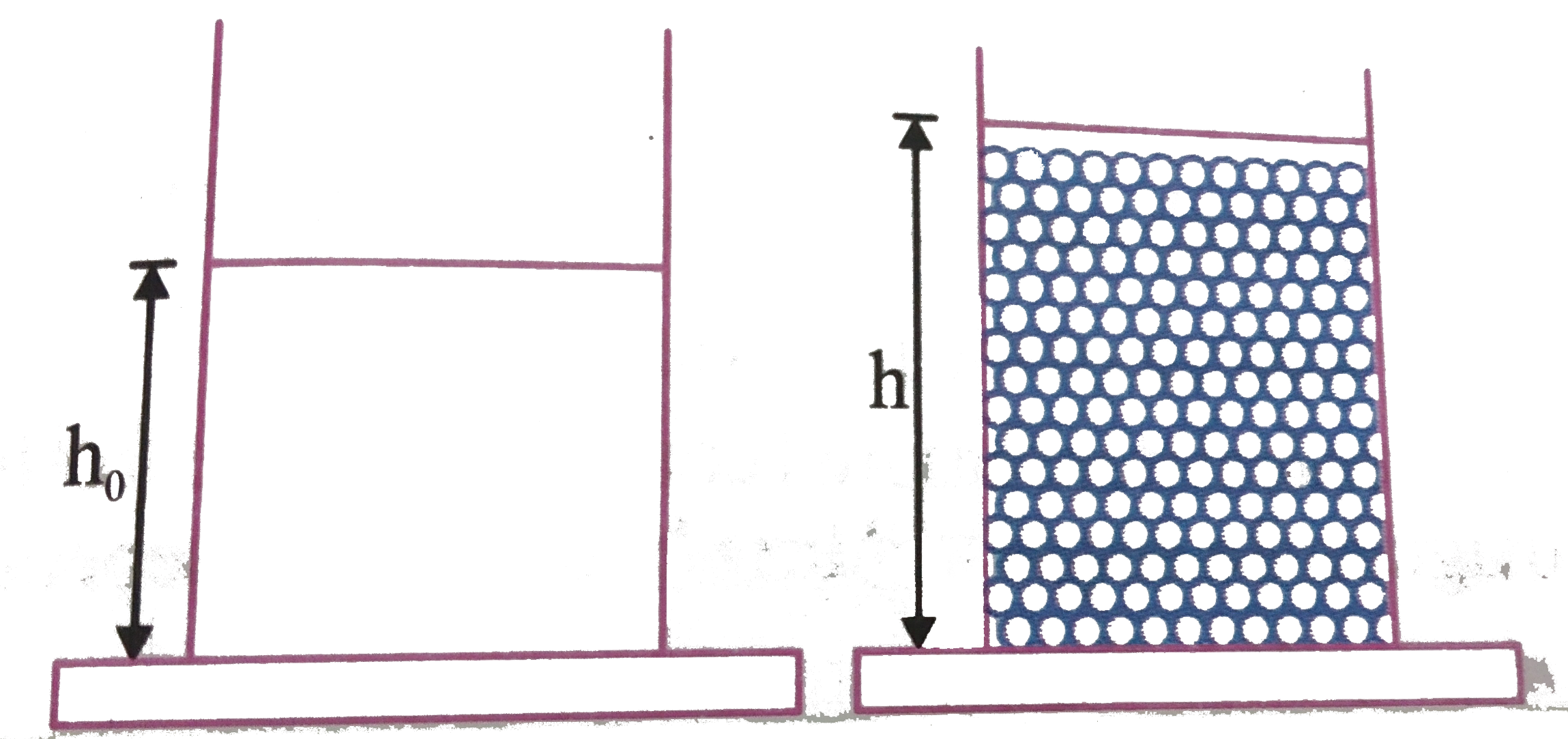
In a cylindrical container water is filled up to a height of h0=1.0m. Now a large number of small iron balls are gently dropped one by one into the container till the upper layer of the balls touches the water surface. if average density of the contents is ρ=4070kg/m3, density of iron is ρi=7140kg/m3 and density of iron is ρ0=1000kg/m3 find the height h of the water level (in S.I. units) in the container with the iron balls.
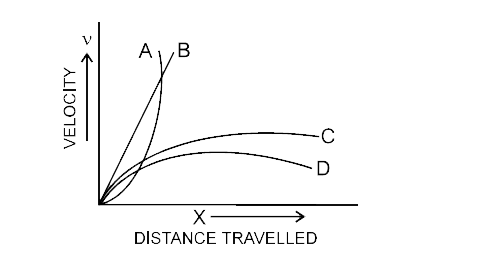
View SolutionA small spherical solid balls is dropped in a viscous liquid. Its journey in the liquid is best described in the figure by
View SolutionA rubber ball of bulk modulus B is taken to a depth h of a liquid of density ρ. Find the fractional change in the radius of the ball.
View SolutionAn object of w and density ρ is submerged in liquid of density σ, its apparent weight will be
View Solution
