A potentiometer shows reading of 38cm when connected with 1.2V battery the the same potentiometer is connected to a 1.8V battery. Find difference in length.
To solve the problem step by step, we will use the concept of a potentiometer, which states that the potential difference across the wire is directly proportional to the length of the wire.
1. Identify Given Values:
- When connected to a 1.2V battery, the balancing length (L1) is 38 cm.
- The new battery voltage (E2) is 1.8V.
2. Use the Proportionality of Potentiometer:
- According to the potentiometer principle, the relationship between the potential difference and the length of the wire can be expressed as:
E2E1=L2L1
- Here, E1 is the voltage of the first battery (1.2V), L1 is the length corresponding to E1 (38 cm), and L2 is the length corresponding to E2 (1.8V).
3. Substitute the Known Values:
- Substitute the known values into the equation:
1.8V1.2V=L238cm
4. Cross-Multiply to Solve for L2:
- Cross-multiplying gives:
1.8×38=1.2×L2
- Calculate 1.8×38:
1.8×38=68.4
- Now, the equation becomes:
68.4=1.2×L2
5. Solve for L2:
- Divide both sides by 1.2 to find L2:
L2=68.41.2=57cm
6. Calculate the Difference in Length:
- Now, find the difference between L2 and L1:
Difference=L2−L1=57cm−38cm=19cm
Final Answer:
The difference in length when the potentiometer is connected to a 1.8V battery compared to when it is connected to a 1.2V battery is 19 cm.
- When connected to a 1.2V battery, the balancing length (L1) is 38 cm.
- The new battery voltage (E2) is 1.8V.
- According to the potentiometer principle, the relationship between the potential difference and the length of the wire can be expressed as:
E2E1=L2L1
- Here, E1 is the voltage of the first battery (1.2V), L1 is the length corresponding to E1 (38 cm), and L2 is the length corresponding to E2 (1.8V).
- Substitute the known values into the equation:
1.8V1.2V=L238cm
- Cross-multiplying gives:
1.8×38=1.2×L2
- Calculate 1.8×38:
1.8×38=68.4
- Now, the equation becomes:
68.4=1.2×L2
- Divide both sides by 1.2 to find L2:
L2=68.41.2=57cm
- Now, find the difference between L2 and L1:
Difference=L2−L1=57cm−38cm=19cm
The difference in length when the potentiometer is connected to a 1.8V battery compared to when it is connected to a 1.2V battery is 19 cm.
Topper's Solved these Questions
Similar Questions
A potentiometer wire of length 1 m has a resistance of 5Ω. It is connected to a 8 V battery in series with a resistance of 15Ω. Determine the emf of the primary cell which gives a balance point at 60 cm.
View SolutionA potentiometer wire of length 1 m has a resistance of 10Ω. It is connected to a 6V battery in series with a resistance of 5Ω. Determine the emf of the primary cell which gives a balance point at 40cm.
View Solution
Knowledge Check
A potentiometer has a uniform wire of length 10m and resistance 5Ω. The potentiometer is connected to an across a cell of e.m.f. 2 V and internal resistanc 10Ω. The reading of voltmeter is
A1mV/mB5mV/mC0.1 mV/mD4 mV/cmwhen a copper votameter is connected with a battery of emf 12V,2g of copper is deposite in 30 min. if the same voltmeter is connected across a 6V battery then the mass of copper deposite in 45 min would be
A1gB1.5gC2gD2.5gWhen copper voltmeter is connected with a battery of emf 12 V, 2 g of copper is deposited in 30 min. If the same voltmeter is connected across a 6 V battery, then the mass of copper deposited in 45 min would be
A1 gB1.5 gC2 gD2.5 g
A potentiometer wire of length 1.0 m has a resistance of 10Ω. It is connected to a 6 V battery in seried with a resistance of 5Ω. Determine the emf of the primary cell which gives a balance point at 40 cm.
View SolutionA potentiometer wire of length 1 m has a resistance of 10 Ω . It is connected to a 6 V battery in series with a resistance of 5 Ω . Determine the emf of the primary cell which gives a balance point at 40 cm.
View SolutionA potentiometer wire of length 1.0 m has a resistance of 15 ohm. It is connected to a 5 V source in series with a resistance of 5Ω. Determine the emf of the primary cell which has a balance point at 60 cm.
View SolutionIn fig. battery E is balanced on 55cm length of potentiometer wire but when a resistance of 10Ω is connected in parallel with the battery then it balances on 50cm length of the potentiometer wire then internal resistance r of the battery is:-
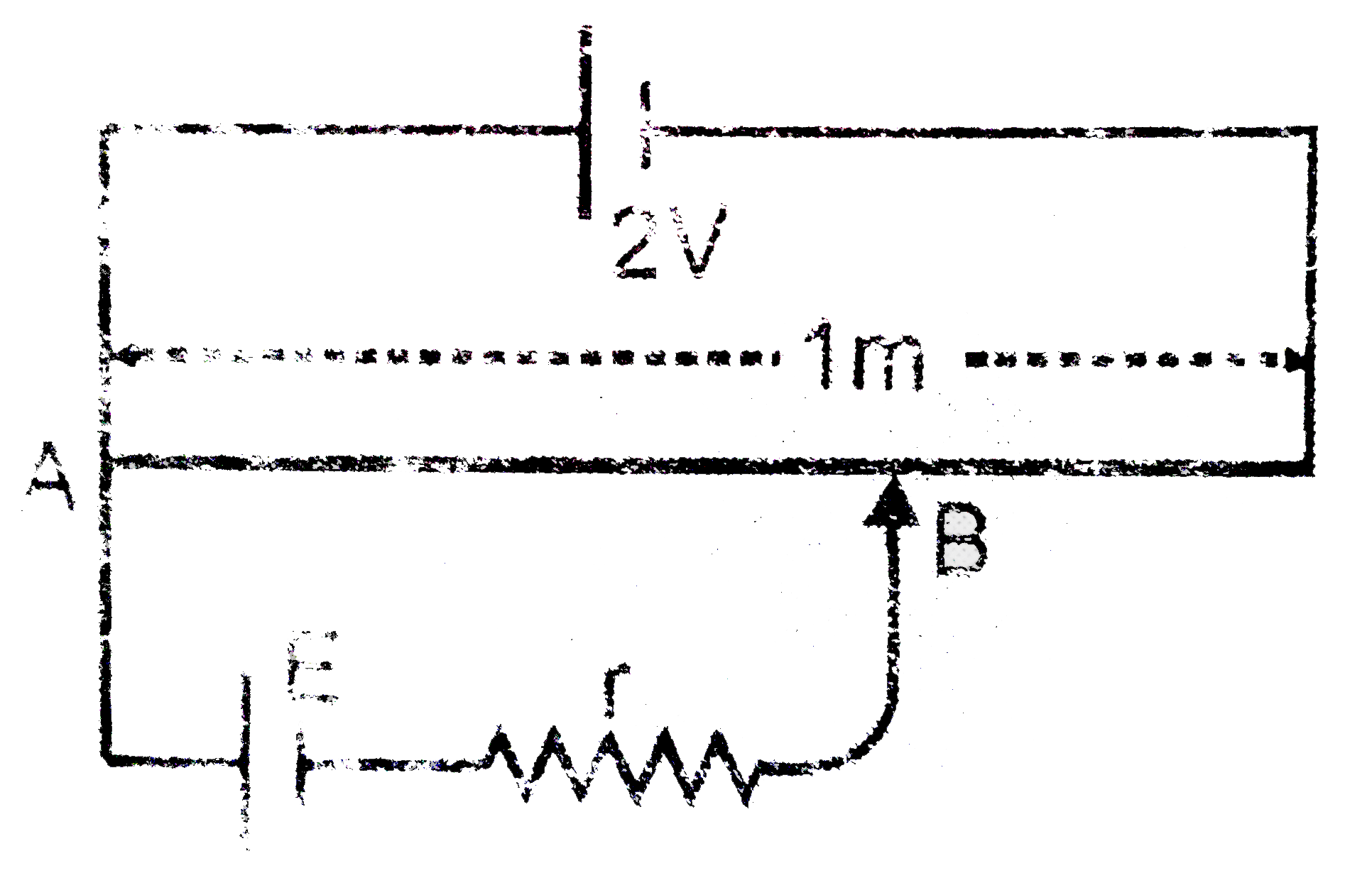
View SolutionA 2 V battery, a 990Ω resistor and a potentiometer of 2 m length, all are connected in series of the resistance of potentiometer wire is 10Ω, then the potential gradient of the potentiometer wire is
View Solution
