Find radius of gyration about an axis passing through midpoint of thin rod (L=10√3) 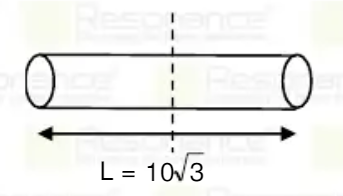
2m
3m
5m
8m
Step by step video & image solution for Find radius of gyration about an axis passing through midpoint of thin rod (L=10sqrt(3)) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Three identical rods, each of length l, are joined to form a rigid equilateral triangle. Its radius of gyration about an axis pássing through a corner and perpendicular to the plane of the triangle is l√x. Find x.
View SolutionRadius of gyration of a body about an axis at a distance 6 cm from it COM is 10 cm . Its radius of gyration about a parallel axis passing through its COM is (n) cm . find value of n.
View Solution
Knowledge Check
A thin uniform rod of mass M and length L. Find the radius of gyration for rotation about an axis passing through a point at a distance ofL4 from centre and perpendicular to rod.
A√748LB√548LC√724LD√1924LThe radius of of disc is 2 m the radius of gyration of disc about an axis passing through its diameter is
A2 mB2 cmC1 mD0.2 mRadius of gyration of a ring about a transverse axis passing through its centre is
A0.5× diameter of ringBdiameter of ringC2× diameter of ringD(diameter of ring)2
Three identical rods, each of length L, are joined to form a rigid equilateral triangle. Its radius of gyration about an axis passing thorugh a corner and perpendicular to plane of triangle is
View SolutionThe moment of inertia of a uniform thin rod of length L and mass M about an axis passing through a point at a distance of L3 from one of its ends and perpendicular to the rod is
View SolutionThe radius of gyration of a uniform rod of length l about an axis passing through one of its ends and perpendicular to its length is
View SolutionThe radius of gyration of a disc of mass 100 g and radius 5 cm about an axis passing through its centre of gravity and perpendicular to the plane is
View SolutionThe radius of gyration of a uniform disc of radius R, about an axis passing through a point R2 away from the centre of disc, and perpendicular to the plane of disc is:
View Solution
