A ball of mass m=0.15kg moving with speed 12m/s collide elastically with wall and rebound with same speed, if force applied by wall is 100N. Then, the time of collision
a. 0.025s
b. 0.036s
c. 0.005s
d. 0.018s
To solve the problem, we need to determine the time of collision of a ball with a wall, given its mass, initial speed, and the force exerted by the wall. The ball rebounds elastically, meaning it retains the same speed but in the opposite direction after the collision.
1. Identify Given Values:
- Mass of the ball, m=0.15kg
- Initial speed of the ball, v=12m/s
- Force exerted by the wall, F=100N
2. Determine Change in Momentum:
- The initial momentum of the ball before collision is:
pinitial=m⋅v=0.15kg⋅12m/s=1.8kg m/s
- After colliding elastically, the ball rebounds with the same speed but in the opposite direction, so its final momentum is:
pfinal=m⋅(−v)=0.15kg⋅(−12m/s)=−1.8kg m/s
- The change in momentum (Δp) is given by:
Δp=pfinal−pinitial=−1.8kg m/s−1.8kg m/s=−3.6kg m/s
3. Calculate the Time of Collision:
- The relationship between force, change in momentum, and time is given by:
F=ΔpΔt
- Rearranging for Δt:
Δt=2ΔpF
- Substituting the values:
Δt=2×3.6kg m/s100N=7.2kg m/s100N=0.072s
4. Final Calculation:
- Since we have calculated the total change in momentum, we need to divide by the force to find the time:
Δt=3.6100=0.036s
Conclusion:
The time of collision is Δt=0.036s.
- Mass of the ball, m=0.15kg
- Initial speed of the ball, v=12m/s
- Force exerted by the wall, F=100N
- The initial momentum of the ball before collision is:
pinitial=m⋅v=0.15kg⋅12m/s=1.8kg m/s
- After colliding elastically, the ball rebounds with the same speed but in the opposite direction, so its final momentum is:
pfinal=m⋅(−v)=0.15kg⋅(−12m/s)=−1.8kg m/s
- The change in momentum (Δp) is given by:
Δp=pfinal−pinitial=−1.8kg m/s−1.8kg m/s=−3.6kg m/s
- The relationship between force, change in momentum, and time is given by:
F=ΔpΔt
- Rearranging for Δt:
Δt=2ΔpF
- Substituting the values:
Δt=2×3.6kg m/s100N=7.2kg m/s100N=0.072s
- Since we have calculated the total change in momentum, we need to divide by the force to find the time:
Δt=3.6100=0.036s
The time of collision is Δt=0.036s.
Topper's Solved these Questions
Similar Questions
A ball of mass 2 kg is moving with velocity 20 m/sec strikes with the surface and rebounds with same speed, if time of contact is 0.1 sec then calculate average force on the ball.
View SolutionA ball of mass 2kg moving with speed 5m/s collides directly with another ball of mass 3kg moving in the same direction with speed 4m/s. The coefficient os restitution is 2/3. Find the velocities of both ball after the collision.
View Solution
Knowledge Check
A ball of mass m moving with a speed u0 collides elastically with a rod of mass M suspended in the vertical plane by the hinge O. The rod is free to rotate in the vertical plane. Before and after the collision.
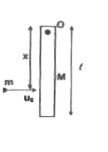 ALinear momentum of the ball and rod system is conservedBLinear momentum of the ball and rod system is conserved only when the collision is elasticCLinear momentum of the ball and rod system may be conserved for a particular value of x.Dnone of these
ALinear momentum of the ball and rod system is conservedBLinear momentum of the ball and rod system is conserved only when the collision is elasticCLinear momentum of the ball and rod system may be conserved for a particular value of x.Dnone of theseA ball of mass m moves with speed v and stricks a wall having infinite mass and it returns with same speed then the work done by the ball on the wall is
AZeroBmvjoe–sCm/vjoe–sDv/mjoe–sA ball of mass 250 g moving with 20 m/s strikes a vertical wall and rebounds along the same line with a velocity of 15 m/s. If the time of contact is 0.1 s, the force exerted by the wall on the ball is
A87.5 NB12.5 NC−12.5 ND−87.5 N
A ball of mass 'm' strikes a rigid wall with speed 'u' and rebounds with the same speed. The impulse imparted to the ball by the wall is
View SolutionIf two balls each of mass 0.06kg moving in opposite directions with speed 4m/s collide and rebound with the same speed , then the impulse imparted to each ball due to other is
View SolutionIf two balls each of mass 0.06kg moving in opposite directions with speed 4m/s collide and rebound with the same speed , then the impulse imparted to each ball due to other is
View SolutionA ball A of mass 1kg , moving with a speed of 12m/s , collides obliquely and elasticity with another ball B which was initially at rest. Ball A then moves off at the right angle to its initial direction with a speed of 5m/s. The momentum of ball B after the collision is
View SolutionA ball of mass 0.5kg moving with a velocity of 2m/s strikes a wall normally and bounces back with the same speed . If the time of contact between the ball and the wall is 1 millisecond , the average force exerted by the wall on the ball is
View Solution
