The remainder of (2021)2022+(2022)2021 when divided by 7 is
0
1
2
6
To find the remainder of (2021)2022+(2022)2021 when divided by 7, we can simplify the bases first by finding their remainders when divided by 7.
Step 1: Find the remainders of the bases
1. Calculate 2021mod7:
2021÷7=288(integer part)
2021−(288×7)=2021−2016=5
So, 2021≡5mod7.
2. Calculate 2022mod7:
2022÷7=288(integer part)
2022−(288×7)=2022−2016=6
So, 2022≡6mod7.
Step 2: Rewrite the expression using the remainders
Now we can rewrite the original expression:
(2021)2022+(2022)2021≡(5)2022+(6)2021mod7
Step 3: Calculate 52022mod7
To find 52022mod7, we can use Fermat's Little Theorem, which states that if p is a prime and a is not divisible by p, then:
ap−1≡1modp
Here, p=7 and a=5:
56≡1mod7
Now, we need to find 2022mod6:
2022÷6=337(integer part)
2022−(337×6)=2022−2022=0
Thus, 2022≡0mod6. Therefore:
52022≡(56)337⋅50≡1337⋅1≡1mod7
Step 4: Calculate 62021mod7
Similarly, for 62021mod7:
66≡1mod7
Now, we need to find 2021mod6:
2021÷6=336(integer part)
2021−(336×6)=2021−2016=5
Thus, 2021≡5mod6. Therefore:
62021≡65mod7
Now we calculate 65mod7:
61≡6mod7
62≡6×6=36≡1mod7
63≡62×6≡1×6≡6mod7
64≡62×62≡1×1≡1mod7
65≡64×6≡1×6≡6mod7
Step 5: Combine the results
Now we combine the results:
(52022+62021)mod7≡(1+6)mod7≡7mod7≡0
Final Answer
The remainder of (2021)2022+(2022)2021 when divided by 7 is 0.
1. Calculate 2021mod7:
2021÷7=288(integer part)
2021−(288×7)=2021−2016=5
So, 2021≡5mod7.
2022÷7=288(integer part)
2022−(288×7)=2022−2016=6
So, 2022≡6mod7.
Now we can rewrite the original expression:
(2021)2022+(2022)2021≡(5)2022+(6)2021mod7
To find 52022mod7, we can use Fermat's Little Theorem, which states that if p is a prime and a is not divisible by p, then:
ap−1≡1modp
Here, p=7 and a=5:
56≡1mod7
Now, we need to find 2022mod6:
2022÷6=337(integer part)
2022−(337×6)=2022−2022=0
Thus, 2022≡0mod6. Therefore:
52022≡(56)337⋅50≡1337⋅1≡1mod7
Similarly, for 62021mod7:
66≡1mod7
Now, we need to find 2021mod6:
2021÷6=336(integer part)
2021−(336×6)=2021−2016=5
Thus, 2021≡5mod6. Therefore:
62021≡65mod7
Now we calculate 65mod7:
61≡6mod7
62≡6×6=36≡1mod7
63≡62×6≡1×6≡6mod7
64≡62×62≡1×1≡1mod7
65≡64×6≡1×6≡6mod7
Now we combine the results:
(52022+62021)mod7≡(1+6)mod7≡7mod7≡0
The remainder of (2021)2022+(2022)2021 when divided by 7 is 0.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
Let r be the remainder when 20212020 is divided by 20202. Then r lies between
A0 and 5B10 and 15C20 and 100D107 and 120 - Question 2 - Select One
The remainder when the determinant
∣∣ ∣ ∣∣201420142015201520162016201720172018201820192019202020202021202120222022∣∣ ∣ ∣∣
is divided by 5 is-A1B2C3D4 - Question 3 - Select One
If λ is the remainder when 22021 is divided by 17, then the value of λ must be equal to
A3B7C13D15
Let r be the remainder when 20212020 is divided by 20202. Then r lies between
View SolutionWhen x is divided by 4 leaves remainder 3 then (2022+x)2022 is divisided by 8 , remainder is
View SolutionThere is a remainder of 4 when a number is divided by 7. What will be the remainder if the square of the same number is divided by 7?
View SolutionA number which when divided by 10 leaves remainder of 9,when divided by 9 leaves remainder of 8 and when divided by 8 leaves a remainder of 7 is
View SolutionA number which when divided by 10 leaves a remainder of 9, when divided by 9 leaves a remainder of 8, and when divided by 8 leaves a remainder of 7 , is :
View Solution


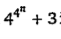 is divided by 7 is:
is divided by 7 is: