A bullet is projected vertically downwards with initial velocity 100m/s from tower. It reaches on ground after 10s. Bullet sticks to ground after collision. Choose correct option for graph between velocity and time for first 20s of motion of bullet.
a. 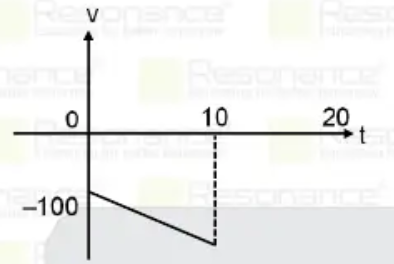
b. 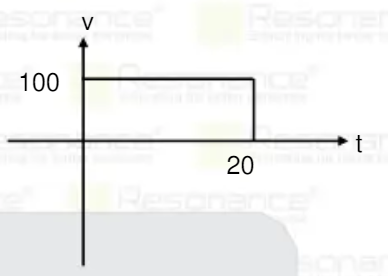
c.
d.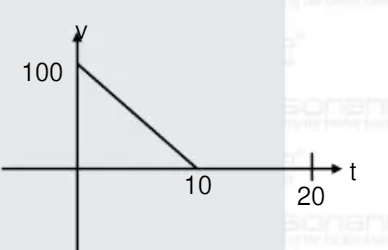
To solve the problem, we need to analyze the motion of the bullet projected vertically downwards with an initial velocity of 100 m/s and determine the velocity-time graph for the first 20 seconds of its motion.
1. Identify the Initial Conditions:
- Initial velocity (u) = 100 m/s (downwards)
- Time of flight (t) = 10 seconds
- Acceleration due to gravity (g) = 9.8 m/s² (downwards)
2. Calculate the Final Velocity Just Before Impact:
We can use the equation of motion:
v=u+at
where:
- v = final velocity
- a = acceleration (which is g = 9.8 m/s²)
Plugging in the values:
v=100m/s+(9.8m/s2×10s)=100m/s+98m/s=198m/s
3. Determine the Velocity After Impact:
Since the bullet sticks to the ground after the collision, its velocity becomes 0 m/s immediately after the impact.
4. Construct the Velocity-Time Graph:
- From 0 to 10 seconds, the velocity increases linearly from 100 m/s to 198 m/s.
- At 10 seconds, the bullet hits the ground, and the velocity drops to 0 m/s instantly.
- From 10 to 20 seconds, the velocity remains at 0 m/s since the bullet is stuck in the ground.
5. Graph Characteristics:
- The graph will show a linear increase in velocity from 100 m/s to 198 m/s over the first 10 seconds.
- At 10 seconds, there will be a sudden drop to 0 m/s, and the velocity will remain constant at 0 m/s from 10 to 20 seconds.
Conclusion:
The correct option for the velocity-time graph will show:
- A straight line with a positive slope from (0, 100) to (10, 198).
- A vertical drop to (10, 0) and then a horizontal line at 0 m/s from (10, 0) to (20, 0).
- Initial velocity (u) = 100 m/s (downwards)
- Time of flight (t) = 10 seconds
- Acceleration due to gravity (g) = 9.8 m/s² (downwards)
We can use the equation of motion:
v=u+at
where:
- v = final velocity
- a = acceleration (which is g = 9.8 m/s²)
v=100m/s+(9.8m/s2×10s)=100m/s+98m/s=198m/s
Since the bullet sticks to the ground after the collision, its velocity becomes 0 m/s immediately after the impact.
- From 0 to 10 seconds, the velocity increases linearly from 100 m/s to 198 m/s.
- At 10 seconds, the bullet hits the ground, and the velocity drops to 0 m/s instantly.
- From 10 to 20 seconds, the velocity remains at 0 m/s since the bullet is stuck in the ground.
- The graph will show a linear increase in velocity from 100 m/s to 198 m/s over the first 10 seconds.
- At 10 seconds, there will be a sudden drop to 0 m/s, and the velocity will remain constant at 0 m/s from 10 to 20 seconds.
The correct option for the velocity-time graph will show:
- A straight line with a positive slope from (0, 100) to (10, 198).
- A vertical drop to (10, 0) and then a horizontal line at 0 m/s from (10, 0) to (20, 0).
Topper's Solved these Questions
Similar Questions
A ball is thrown vertically downward with velocity of 20 m/s from top of tower. It hits ground after some time with a velocity of 80 m /s . Height of tower is
View SolutionAn object is thrwon vertically upwards with a velocity of 60 m/s. After what time it strike the ground ? Use g=10m/s2.
View Solution
Knowledge Check
An object is projected upwards with a velocity of 100m/s. It will strike the ground after (approximately)
A10secB20secC15secD5secA ball is thrown vertically downward with a velocity of 20m/s from the top of a tower,It hits the ground after some time with a velocity of 80m/s .The height of the tower is : (g=10mg2)
A340 mB230 mC300 mD360 mA body is thrown horizontally from the top of a tower. It reaches the ground after 4s at an angle 45∘ to the ground. The velocity of projection is
A9.8ms−1B19.6ms−1C29.4ms−1D39.2ms−1
A ball is thrown vertically downward with a velocity of 20m/s from the top of a tower,It hits the ground after some time with a velocity of 80m/s .The height of the tower is : (g=10mg2)
View SolutionA ball is thrown vertically upward with velocity 20m/s from a tower of height 60 m. After how much time and with what velocity will it strike the ground?
View SolutionA particle is projected vertically upwards from ground with velocity 10 m/s. Find the time taken by it to reach at the highest point ?
View SolutionA piece of wood of mass 0.03 kg is dropped from the top of a building 100 m high. At the same time, a bullet of mass 0.02 kg is fired vertically upward with a velocity of 100 m/s from the ground the bullet gets embedded in the wooded piece after striking. find the height to which the combination rises above the building before it starts falling take g=10m/s2
View SolutionA stone is thrown downwards with velocity 10 m/s from the roof of a builng and it reaches the ground with speed 40 m/s. the height of the building would be
View Solution
