Two players P1 and P2 play a game against each other . In every round of the game , each player rolls a fair the once , where the six faces of the die have six distinct numbers . Let x and y denote the readings on the die rolled by P1 and P2 respectively . if x>y , then P1 scores 5 points and P2 scores 0 point . if x = y , then each player scores 2 points . if x<y , then P1 scores 0 point and P2 scores 5 points . Let Xi and Yi be the total scores of P1 and P2 respectively , after playing the ith round .
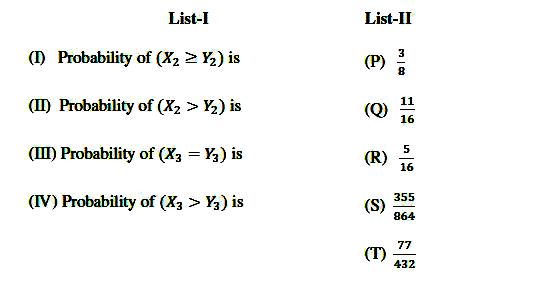
The correct option is :
(I)→(Q),(II)→(R),(III)→(T),(IV)→(S)
(I)→(Q),(II)→(R),(III)→(T),(IV)→(T)
(I)→(P),(II)→(R),(III)→(Q),(IV)→(S)
(I)→(P),(II)→(R),(III)→(Q),(IV)→(T)
Step by step video & image solution for Two players P_(1) and P_(2) play a game against each other . In every round of the game , each player rolls a fair the once , where the six faces of the die have six distinct numbers . Let x and y denote the readings on the die rolled by P_(1) and P_(2) respectively . if x gt y , then P_(1) scores 5 points and P_(2) scores 0 point . if x = y , then each player scores 2 points . if x lt y , then P_(1) scores 0 point and P_(2) scores 5 points . Let X_(i) and Y_(i) be the total scores of P_(1) and P_(2) respectively , after playing the i^(th) round . The correct option is : by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- JEE ADVANCED 2022BOOK - JEE ADVANCED PREVIOUS YEARCHAPTER - JEE ADVANCED 2022EXERCISE - MATHEMATICS (SECTION -2)
6 Videos
- JEE ADVANCED 2021BOOK - JEE ADVANCED PREVIOUS YEARCHAPTER - JEE ADVANCED 2021EXERCISE - QUESTION
38 Videos
- MOCK TEST 2022BOOK - JEE ADVANCED PREVIOUS YEARCHAPTER - MOCK TEST 2022EXERCISE - Question
18 Videos
Similar Questions
66 games were played in a tournament where each player placed one against the rest. The number of players are
View SolutionA die has two faces each with number 1, three faces each with number 2 and one face with number 3. If the die rolled once, determine (i)P(1) (ii) P(1or3) (iii) P(not3)
View Solution
Knowledge Check
Football teams T1 and T2 have to play two games against each other. It is assumed that the outcomes of the two games are independent. The probabilities of T1 winning,drawing and losing a game against T2 are 12,16 and 13, respectively. Each teams gets 3 points for a win, 1 point of a drawn and 0 point for a loss in a games.
P(X=Y) isA1136B13C1336D12In a badminton each player played one game with ll the other players. Number of players participated in the tournament if they played 105 games is
A35B15C12D10Football teams T1 and T2 have to play two games against each other. It is assumed that the outcomes of the two games are independent. The probabilities of T1 winning,drawing and losing a game against T2 are 12,16 and 13, respectively. Each teams gets 3 points for a win, 1 point of a drawn and 0 point for a loss in a games.
P(X>T) isA14B512C12D712
8n players P1,P2,P3,....,P8n play a knock out tournament. It is known that all the players are of equal strngth. The tournat random is held in three rounds where the players are paired at random in each rouns. If it is given that P1 wins in the third round. Find the probability than P2 loses in the second round.
View SolutionPlayers P1,P2,P3,P4 toss a fair coin one after another independently till a player gets a head. If P1 starts the toss, what is the probability that P1 will get head first?
View SolutionFootball teams T1andT2 have to play two games are independent. The probabilities of T1 winning, drawing and lossing a game against T2 are 16,16and13, respectively. Each team gets 3 points for a win, 1 point for a draw and 0 point for a loss in a game. Let X and Y denote the total points scored by teams T1andT2 respectively, after two games.
P(X=Y) is
View SolutionFootball teams T1andT2 have to play two games against each other. It is assumed that the outcomes of the two games are independent. The probabilities of T1 winning, drawing and losing a game against T2 are 12,16and13 respectively. Each team gets 3 points for a win. 1 point for a draw and 0 point for a loss in a game. Let XandY denote the total points scored by teams T1andT2 respectively. after two games. P(X=Y) is
View SolutionFootball teams T1andT2 have to play two games are independent. The probabilities of T1 winning, drawing and lossing a game against T2 are 16,16and13, respectively. Each team gets 3 points for a win, 1 point for a draw and 0 point for a loss in a game. Let X and Y denote the total points scored by teams T1andT2 respectively, after two games.
P(X>Y) is
View Solution
