Let p , q , r be nonzero real numbers that are respectively , the 10th,100th and 1000th terms of a harmonic progression . Consider the system of linear equations
x+y+z=1
10x+100y+1000z=0
qrx+pry+pqz=0
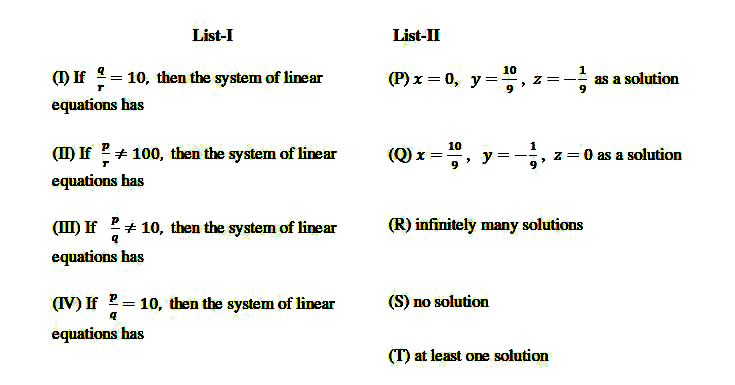
The correct option is :
(I)→(T),(II)→(R),(III)→(S),(IV)→(T)
(I)→(Q),(II)→(S),(III)→(S),(IV)→(R)
(I)→(Q),(II)→(R),(III)→(P),(IV)→(R)
(I)→(T),(II)→(S),(III)→(P),(IV)→(T)
Step by step video & image solution for Let p , q , r be nonzero real numbers that are respectively , the 10^(th) , 100^(th) and 1000^(th) terms of a harmonic progression . Consider the system of linear equations x + y + z = 1 10x + 100y + 1000z = 0 qrx + pr y + pq z = 0 The correct option is : by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- JEE ADVANCED 2022BOOK - JEE ADVANCED PREVIOUS YEARCHAPTER - JEE ADVANCED 2022EXERCISE - MATHEMATICS (SECTION -2)
6 Videos
- JEE ADVANCED 2021BOOK - JEE ADVANCED PREVIOUS YEARCHAPTER - JEE ADVANCED 2021EXERCISE - QUESTION
38 Videos
- MOCK TEST 2022BOOK - JEE ADVANCED PREVIOUS YEARCHAPTER - MOCK TEST 2022EXERCISE - Question
18 Videos
Similar Questions
Knowledge Check
The system of equations x−y+3z=4,x+z=2 x+y−z=0 has
AA unique solutionBFinitely many solutionCInfinitely many solutionsDNone of the aboveThe system of equations ax + y + z = 0 , -x + ay + z = 0 and - x - y + az = 0 has a non-zero solution if the real value of 'a' is
A1B−1C3D0The system of linear equations
x+y+z=1,
x+2y+4z=λ,x+4y+10z=λ2 has a solution if it satisfies the followingAλ=−1Bλ≠1Cλ=2Dλ∈ϕ
Consider the system of equations :
x + y + z = 0
αx+βy+γz=0
α2x+β2y+γ2z=0
then the system of equations has
View SolutionThe system of equations x−y+3z=4,x+z=2 x+y−z=0 has
View SolutionThe number of distinct real values of λ for which the system of linear equations x+y+z=λx,x+y+z=λy,x+y+z+λz has non - trival solution.
View SolutionThe system of linear equations
x + y + z = 0
2xa+3yb+4zc=0
xa+yb+zc=0
has non trivia solution then
View SolutionConsider the system of equations : xsinθ−2ycosθ−az=0, x+2y+z=0, −x+y+z=0, θ∈R
View Solution
