Two concentric circles are centered at O(-4, 3). The ratio of the area of inner circle to that of the outer circle is 1:9. Points A and B lie on the boundaries of the inner and outer circle, respectively, as shown below.
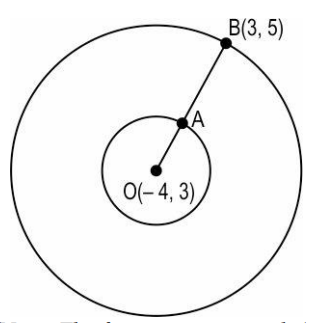
Two concentric circles are centered at O(-4, 3). The ratio of the area of inner circle to that of the outer circle is 1:9. Points A and B lie on the boundaries of the inner and outer circle, respectively, as shown below. (Note: The figure is not to scale.) The coordinates of point B are (3, 5). Which of the following are the coordinates of A?
(Note: The figure is not to scale.)
The coordinates of point B are (3, 5). Which of the following are the coordinates of A?

A

(23,133)

B

(−53,113)

C

(−94,144)

D

(−3310,165)

Video Solution
Doubtnut Promotions Banner
|
Answer

Step by step video & image solution for Two concentric circles are centered at O(-4, 3). The ratio of the area of inner circle to that of the outer circle is 1:9. Points A and B lie on the boundaries of the inner and outer circle, respectively, as shown below. (Note: The figure is not to scale.) The coordinates of point B are (3, 5). Which of the following are the coordinates of A? by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.

Updated on:21/07/2023
Class 10MATHSQUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • The difference in the areas of two concentric circles is 66 cm2 and the radius of the outer circle is 11 cm. What is the radius of the inner circle?

    A8 cm
    B9 cm
    C10 cm
    D7 cm

  • In two Concentric circles, AB and CD are two chords of the outer circle which touch the inner circle at E and F. Then :

    AAB = CD
    BAB=12CD
    CAB≠CD
    DNone of these

  • The ratio of the outer and the inner perimeter of a circular path is 23 : 22. If the path is 5 metres wide, the diameter of the inner circle is :

    A110 m
    B55m
    C220 m
    D230 m