Shown below is a regular hexagon whose two vertices are joined by a vector.
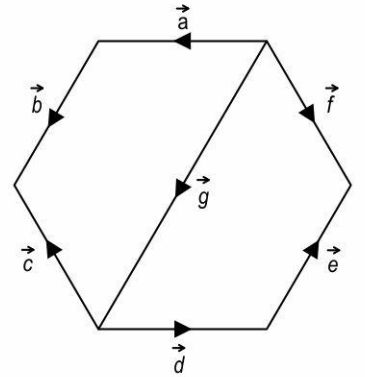
Which of the statement(s) is/are true?
(i) →a and →d are equal vectors. (ii) →b and →e are collinear vectors.
(iii) →c, →d and →g are coinitial vectors.
only (ii)
only (ii)
only (i) and (ii)
all - (i), (ii) and (iii)
Step by step video & image solution for Shown below is a regular hexagon whose two vertices are joined by a vector. Which of the statement(s) is/are true? (i) vec a and vec d are equal vectors. <b> (ii) vec b and vec e are collinear vectors. (iii) vec c, vec d and vec g are coinitial vectors. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
The vectors →a,→b,→c,→d are coplanar then
View Solution.Vectors →A,→B and →c are shown in figure.Find angle between (i) →A and →B. (ii) →A and →C. ,(iii)vec Bandvec C
View Solution→a and →b are two given unit vectors at right angle. The unit vector equally inclined with →a,→b and →a×→b will be
View SolutionThe vectors →Aand→B are such that ∣∣→A+→B∣∣=∣∣→A−→B∣∣ . The angle between the two vectors is
View SolutionShow that the vectors 2→a−→b+3→c,→a+→b−2→cand→a+→b−3→c are non-coplanar vectors (where →a,→b,→c are non-coplanar vectors)
View SolutionIf →a and →b are two vectors such that ∣∣→a+→b∣∣=|→a| , then prove that vector 2→a+→b is perpendicular to vector →b
View Solution→a,→b,→c, dare any four vectors then (→a×→b)×(→c×→d) is a vector Perpendicular to →a,→b,→c,→d
View SolutionIf →a and →b are two non-collinear vectors having the same initial point. What are the vectors represented by →a+→b and →a−→b .
View SolutionVectors →aand→b are non-collinear. Find for what value of n vectors →c=(n−2)→a+→band→d=(2n+1)→a−→b are collinear?
View SolutionIf →a,→c,→d are non-coplanar vectors, then →d.{→a×[→b×(→c×→d)]} is equal to
View Solution
